1. Τροχός στρέφεται γύρω από σταθερό άξονα περιστροφής που είναι κάθετος στις βάσεις του και διέρχεται απ’ τα κέντρα τους με σταθερή γωνιακή ταχύτητα. Ποιες από τις παρακάτω προτάσεις είναι σωστές; 3. Ο τροχός του παρακάτω σχήματος στρέφεται γύρω από οριζόντιο άξονα \[x' x\] που είναι κάθετος στη βάση του και περνά απ’ τα κέντρα τους. Ο τροχός στρέφεται κατά τη φορά των δεικτών του ρολογιού με σταθερή γωνιακή ταχύτητα. Ποιες από τις ακόλουθες προτάσεις είναι σωστές;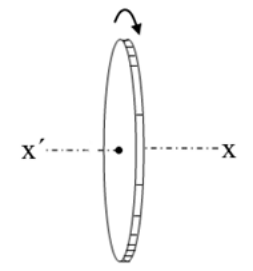
5. Η ράβδος ΟΑ μήκους \[\ell\] του παρακάτω σχήματος στρέφεται γύρω από σταθερό κατακόρυφο άξονα που διέρχεται απ’ το άκρο της Ο. Η στροφική κίνηση της ράβδου είναι ομαλά επιβραδυνόμενη και έχει φορά αντίθετη των δεικτών του ρολογιού.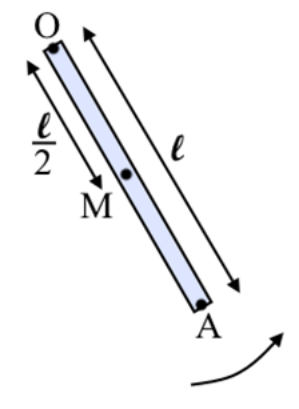
Α. Για τα μέτρα των γραμμικών ταχυτήτων \[υ_Μ, \, υ_Α\] των σημείων Μ, Α την ίδια στιγμή ισχύει:
α) \[υ_Μ=υ_Α\], β) \[υ_Μ=2υ_Α\], γ) \[υ_Α=2υ_Μ\].
Β. Για τα μέτρα των κεντρομόλων επιταχύνσεων \[α_κ\] των σημείων Μ, Α την ίδια στιγμή ισχύει:
α) \[α_{κ_Μ }=α_{κ_Α }\], β) \[α_{κ_Α }=2α_{κ_Μ }\], γ) \[α_{κ_Α }=4α_{κ_Μ }\].
6. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Στην μεταφορική κίνηση ενός στερεού σώματος: 7. Στερεό σώμα εκτελεί στροφική κίνηση γύρω από σταθερό άξονα με σταθερή γωνιακή επιτάχυνση. Δύο σημεία Β και Γ έχουν επιτρόχιες επιταχύνσεις μέτρων \[α_{επ_Β}\] και \[α_{επ_Γ}\] αντίστοιχα και ισχύει \[α_{επ_Γ}=2α_{επ_Β }\].Α) Οι κεντρομόλες επιταχύνσεις των δύο αυτών σημείων την ίδια στιγμή \[t_1\] έχουν μέτρα \[α_{κ_{Γ_1 }}\] και \[α_{κ_{Β_1 }}\] αντίστοιχα και ισχύει:
α) \[ \frac{ α_{κ_{Γ_1 }} } {α_{κ_{Β_1 }} } =\frac{1}{2} \],
β) \[ \frac{ α_{κ_{Γ_1 }} }{ α_{κ_{Β_1 }} } =2\],
γ) \[ \frac{ α_{κ_{Γ_1 }} }{α_{κ_{Β_1 }} } =\frac{1}{4} \],
δ) \[ \frac{ α_{κ_{Γ_1 }} }{ α_{κ_{Β_1 }} } =4\].
Β) Τα μέτρα των επιταχύνσεων \[α_Β,\, α_Γ\] των σημείων Β, Γ αντίστοιχα έχουν λόγο \[\frac{α_Β}{α_Γ}\] ίσο με:
α) \[\frac{1}{2}\], β) \[2\], γ) \[\sqrt{2}\], δ) \[\frac{\sqrt{2} } {2}\].
11. Τροχός στρέφεται γύρω από σταθερό άξονα περιστροφής που είναι κάθετος στις βάσεις του και η γωνιακή του ταχύτητα μεταβάλλεται με σταθερό ρυθμό. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Η \[\vec{α}_{γων}\] του τροχού: 16. Ο ομογενής τροχός του παρακάτω σχήματος στρέφεται γύρω από σταθερό κατακόρυφο άξονα που διέρχεται απ’ το κέντρο του και είναι κάθετο στο επίπεδό του. Την \[t=0\] ο τροχός έχει γωνιακή ταχύτητα \[ω_0>0\] και τότε αποκτά σταθερή \[ \vec{α}_{γων}\] που η κατεύθυνσή της φαίνεται στο σχήμα.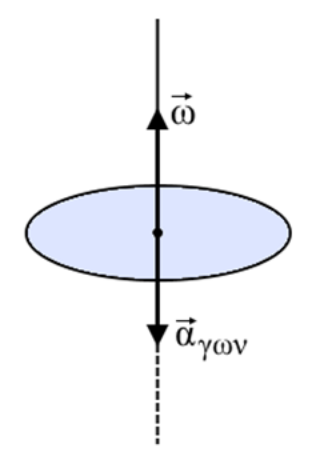
Α) Η χρονική στιγμή \[t_1\] που ο τροχός ακινητοποιείται είναι:
α) \[ \frac{ ω_0 }{ 2|α_{γων} | } \],
β) \[\frac{ 2ω_0}{|α_{γων} |} \],
γ) \[\frac{ω_0}{|α_{γων} |}\] .
Β) Η γωνία που διαγράφει ο τροχός μέχρι τη χρονική στιγμή \[t_1\] είναι:
α) \[ \frac{ω_0^2}{ 2|α_{γων}| } \],
β) \[ \frac{ω_0^2}{|α_{γων} |}\],
γ) \[ \frac{2ω_0^2}{|α_{γων} | }\].
18. Στερεό σώμα εκτελεί στροφική μεταβαλλόμενη κίνηση γύρω από σταθερό άξονα περιστροφής. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή; Όλα τα σημεία του στερεού που κινούνται την ίδια χρονική στιγμή: 21. Ράβδος ΟΑ στρέφεται γύρω από σταθερό άξονα που είναι κάθετος σ’ αυτήν και περνά απ’ το άκρο της Ο. Η στροφική κίνηση γίνεται με σταθερή γωνιακή επιτάχυνση. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή; Το μέτρο της επιτρόχιας επιτάχυνσης ενός σημείου Ζ: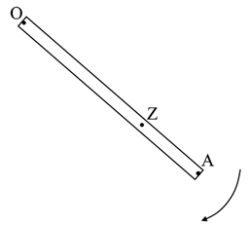
22. Στερεό σώμα στρέφεται γύρω από σταθερό άξονα περιστροφής εκτελώντας ομαλά μεταβαλλόμενη κίνηση. Για την κυκλική κίνηση ενός κινούμενου σημείου του στερεού σώματος, ποιες από τις παρακάτω προτάσεις είναι σωστές; 24. Η ράβδος ΟΑ του παρακάτω σχήματος στρέφεται γύρω από σταθερό οριζόντιο άξονα κάθετο στη διεύθυνσή της που διέρχεται απ’ το άκρο της Ο με τη φορά που φαίνεται στο σχήμα και με σταθερή γωνιακή ταχύτητα.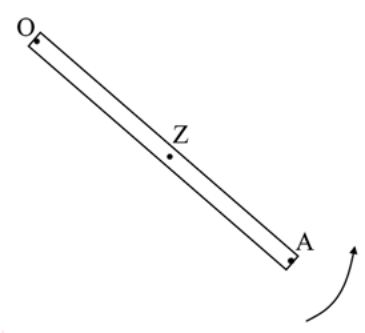
25. Ένα στερεό σώμα εκτελεί μεταφορική κίνηση. Ποια από τις παρακάτω προτάσεις είναι σωστή; 27. Ο ομογενής τροχός ακτίνας \[R\] του παρακάτω σχήματος κυλίεται χωρίς να ολισθαίνει σε οριζόντιο έδαφος και έχει σταθερή γωνιακή ταχύτητα \[ω\]. Η στροφική κίνηση του τροχού έχει φορά αντίθετη της φοράς των δεικτών του ρολογιού. Το σημείο Ζ του τροχού απέχει \[\frac{R}{2}\] απ’ το κέντρο του τροχού. Η ταχύτητα του Ζ όταν αυτό περνά απ’ την κατακόρυφη διάμετρο του τροχού και βρίσκεται πάνω απ’ το κέντρο μάζας του Κ: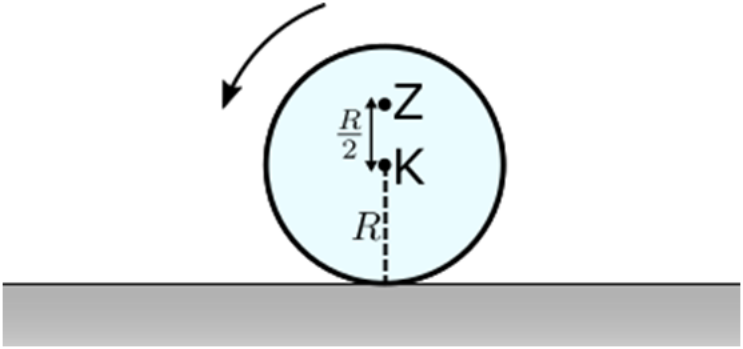
28. Επιλέξτε ποιες από τις παρακάτω προτάσεις είναι σωστές. Η ροπή μιας δύναμης 29. Στερεό σώμα στρέφεται γύρω από σταθερό άξονα περιστροφής. Η γραφική παράσταση της γωνιακής ταχύτητας του στερεού με το χρόνο φαίνεται στο παρακάτω διάγραμμα.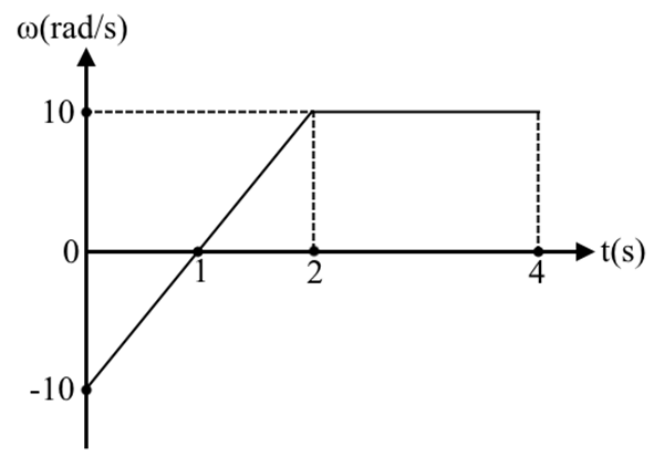
Α) Η γωνιακή μετατόπιση του στερεού απ’ τη στιγμή \[t=0\] ως τη στιγμή \[t=4\, s\] είναι ίση με: α) \[20\, rad\], β) \[30\, rad\], γ) \[40\, rad\].
Β) Ο αριθμός των περιστροφών που διαγράφει ο τροχός ανεξαρτήτως φοράς κίνησης είναι:
α) \[\frac{10}{π}\], β) \[\frac{15}{π}\], γ) \[\frac{20}{π}\].
