1. Σώμα μάζας \[m_1\] εκτελεί α.α.τ. ενέργειας \[Ε_{Τ,1}\] και μέγιστης ταχύτητας \[υ_{max,1}\] πάνω σε λείο οριζόντιο επίπεδο. Όταν το σώμα βρίσκεται στη δεξιά ακραία θέση του συγκρούεται με δεύτερο σώμα μάζας \[m_2=3m_1\] που πριν την κρούση έχει κατακόρυφη ταχύτητα μέτρου \[υ_2\]. Η κρούση είναι πλαστική και το συσσωμάτωμα που προκύπτει εκτελεί και αυτό α.α.τ. με ενέργεια \[Ε_{Τ,2}\] και μέγιστη ταχύτητα \[υ_{max,2}\].
A. Για τις ενέργειες των α.α.τ. ισχύει:
α. \[Ε_{Τ,1}=2Ε_{Τ,2}\].
β. \[ Ε_{Τ,1}=\frac{ Ε_{Τ,2} }{ 2 }\].
γ. \[Ε_{Τ,1}=4Ε_{Τ,2}\].
δ. \[Ε_{Τ,1}=Ε_{Τ,2}\].
Β. Για τις μέγιστες ταχύτητες και ισχύει:
α. \[υ_{max,1}=υ_{max,2}\]
β. \[υ_{max,1}=2υ_{max,2}\]
γ. \[υ_{max,1}=\frac{ υ_{max,2} }{ 2 }\]
δ. \[υ_{max,1}=3υ_{max,2}\]
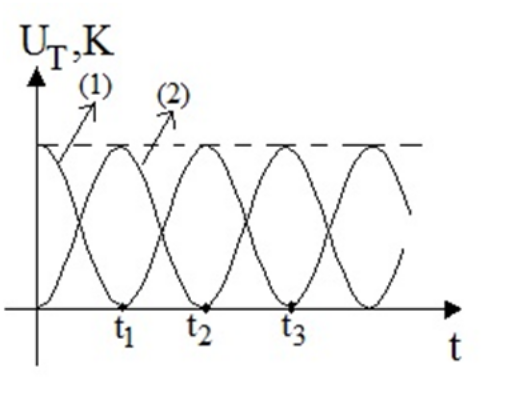
2. Ένα κρυστάλλινο ποτήρι μπορεί να σπάσει λόγω ενός ηχητικού κύματος όταν: 5. Σώμα ισορροπεί ακίνητο και δεμένο στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς \[k\], το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο σε οροφή. Το σώμα δέχεται τη δύναμη του ελατηρίου και το βάρος του. Ανυψώνω το σώμα κατακόρυφα μέχρι το ελατήριο ν’ αποκτήσει το φυσικό του μήκος και απ’ τη θέση αυτή το αφήνω να εκτελέσει α.α.τ. Η επιμήκυνση του ελατηρίου στη Θ.Ι. του σώματος είναι ίση με \[Δ\ell\]. Ποιες απ’ τις επόμενες προτάσεις είναι σωστές; 8. Τρία σώματα με ίσες μάζες \[m_1 = m_2 = m_3 = 1\, kg\] έχουν προσδεθεί στα κάτω άκρα κατακόρυφων ιδανικών ελατηρίων που τα πάνω άκρα τους στερεώνονται σε οριζόντια μεταλλική ράβδο όπως φαίνεται στο παρακάτω σχήμα. Τα ελατήρια έχουν σταθερές \[k_1 = 25 \frac Nm,\, k_2=100 \frac Nm\] και \[k_3=200 \frac Nm\] αντίστοιχα. Με τη βοήθεια κατακόρυφης περιοδικής δύναμης που ασκώ στη ράβδο, εξαναγκάζω τα τρία συστήματα σε ταλάντωση. Η συχνότητα της διεγείρουσας δύναμης είναι σταθερή και ίση με \[f_δ=\frac{5}{π} Hz\], ενώ η ράβδος παραμένει συνεχώς οριζόντια. Η σταθερά απόσβεσης είναι μικρή και για τα τρία συστήματα.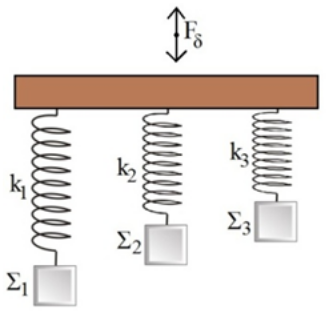
Α. Για τις συχνότητες ταλάντωσης των τριών συστημάτων ισχύει:
α) \[f_3 > f_2 > f_1\]. β) \[ f_1 > f_2 > f_3\]. γ) \[ f_1 = f_2 = f_3\].
B. Για τα πλάτη ταλάντωσης των τριών συστημάτων ισχύει:
α) το Σ1 έχει το μεγαλύτερο πλάτος.
β) το Σ2 έχει το μεγαλύτερο πλάτος.
γ) το Σ3 έχει το μεγαλύτερο πλάτος.
δ) και τα τρία σώματα έχουν ίσα πλάτη.
Γ. Αν αυξήσω τη συχνότητα της διεγείρουσας δύναμης, τότε το πλάτος του σώματος Σ1:
α) θα αυξηθεί. β) θα μειωθεί. γ) θα μείνει σταθερό.
10. Στα κάτω άκρα ιδανικών κατακόρυφων ελατηρίων έχουν προσδεθεί σώματα μάζας \[m_1=m,\, m_2=4m\] και \[m_3=\frac m2\] αντίστοιχα. Τα πάνω άκρα των ελατηρίων στερεώνονται σε ελαστική χορδή όπως φαίνεται στο παρακάτω σχήμα. Ασκώ στη χορδή κατακόρυφη περιοδική δύναμη σταθερής συχνότητας \[f_δ\]. Έτσι τα σώματα αρχίζουν να εκτελούν εξαναγκασμένες ταλαντώσεις και διαπιστώνω ότι τα σώματα με μάζες \[m_2,\, m_3\] ταλαντώνονται με μέγιστο πλάτος.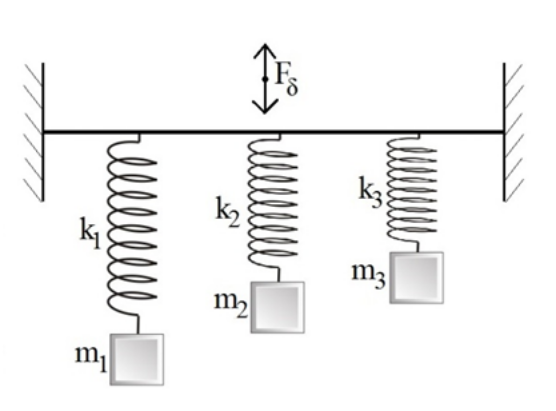
Α. Για τις συχνότητες των τριών ταλαντώσεων ισχύει: α) \[f_1 < f_2 = f_3\]. β) \[f_2=f_3 < f_1\]. γ) \[f_1 = f_2 = f_3\].
Β. Για τις σταθερές των ελατηρίων \[k_2\] και \[k_3\] ισχύει:
α) \[k_2 = 8 k_3\]. β) \[k_2 =4 k_3\]. γ) \[k_2=16 k_3\].
Γ. Αν γνωρίζω ότι \[k_1=k_2\] και αρχίζω να αυξάνω αργά τη συχνότητα της διεγείρουσας δύναμης τότε το πλάτος της ταλάντωσης του ταλαντωτή με μάζα \[m_1\] αρχικά:
α) θα αυξάνεται. β) θα μειώνεται. γ) θα μένει σταθερό.
13. Στο παρακάτω διάγραμμα φαίνεται η μεταβολή της δυναμικής ενέργειας μιας α.α.τ. σε συνάρτηση με το χρόνο. Ποιες από τις παρακάτω προτάσεις είναι σωστές;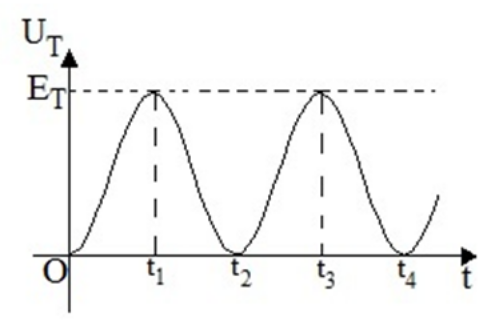
16. Το κτίριο στη διάρκεια ενός σεισμού κινδυνεύει να καταστραφεί όταν: 20. Ταλαντωτής εκτελεί α.α.τ. και η τροχιά που διαγράφει φαίνεται στο παρακάτω σχήμα. Η περίοδος της ταλάντωσης είναι \[Τ\] και το πλάτος της \[Α\], ενώ έχει αρχική φάση \[\frac{π}{2}\]. Το σημείο Γ βρίσκεται στη θέση \[x_Γ=-\frac{Α}{2}\]. Ποιες από τις παρακάτω προτάσεις είναι σωστές;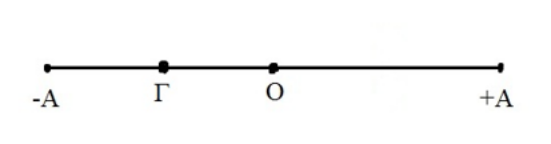
27. Σε μια φθίνουσα μηχανική ταλάντωση που η δύναμη αντίστασης στην κίνηση συνδέεται με την ταχύτητα του ταλαντωτή σύμφωνα με τη σχέση \[F_{αν}=-bυ\], η περίοδος της φθίνουσας ταλάντωσης: 29. Στο παρακάτω σχήμα φαίνεται η μεταβολή της δυναμικής και της κινητικής ενέργειας ενός απλού αρμονικού ταλαντωτή με το χρόνο. Η αρχική φάση της ταλάντωσης είναι \[φ_0=\frac{π}{2}\]. Ποιες από τις παρακάτω προτάσεις είναι σωστές;