1. Στο άκρο ιδανικού ελατηρίου σταθεράς \[k\] έχουμε συνδέσει σώμα μάζας \[m_1=m\] που με τη σειρά του είναι συνδεμένο μέσω αβαρούς και μη εκτετού νήματος με δεύτερο σώμα μάζας \[m_2=m\]. Το συνολικό σύστημα εκτελεί εξαναγκασμένη ταλάντωση με τη βοήθεια τροχού-διεγέρτη που έχει σταθερή συχνότητα \[f_δ=\frac{1}{2π} \sqrt{\frac km}\] . Κάποια χρονική στιγμή κόβουμε το νήμα και το σώμα μάζας \[m_1\] εξακολουθεί να εκτελεί εξαναγκασμένη ταλάντωση.Α) Αν οι συχνότητες των ταλαντώσεων πριν και μετά το κόψιμο του νήματος είναι αντίστοιχα \[f_1\] και \[f_2\] τότε ισχύει:
α) \[f_1=\frac{1}{2π} \sqrt{ \frac{k}{2m} }\] , \[f_2=\frac{1}{2π} \sqrt{ \frac km }\].
β) \[ f_1 = f_2 = \frac{1}{2π} \sqrt{\frac{k}{2m}} \].
γ) \[f_1 = f_2 = \frac{1}{2π} \sqrt{\frac{ k }{ m } } \].
Β) Αν τα πλάτη των ταλαντώσεων πριν και μετά το κόψιμο του νήματος είναι αντίστοιχα \[A_1,\, A_2\] τότε ισχύει:
α) \[Α_1 = Α_2\]. β) \[ Α_2 > Α_1 \]. γ) \[Α_1 > Α_2\].
2. Σώμα εκτελεί φθίνουσα μηχανική ταλάντωση που το πλάτος της μειώνεται με το χρόνο σύμφωνα με τη σχέση \[Α=Α_0 e^{-Λt}\] όπου \[Λ\] θετική σταθερά. Ποιες από τις επόμενες προτάσεις είναι σωστές; Ο χρόνος υποδιπλασιασμού του πλάτους \[t_{ \frac{1}{2} }\]: 3. Σε μια εξαναγκασμένη μηχανική ταλάντωση με σταθερή συχνότητα, ποιες απ’ τις παρακάτω προτάσεις είναι σωστές; 4. Σε μια φθίνουσα μηχανική ταλάντωση η αντιτιθέμενη δύναμη είναι της μορφής \[F_{αν}=-bυ\], όπου \[b\] η σταθερά απόσβεσης. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Αν αυξήσω τη σταθερά απόσβεσης \[b\]: 5. Σε μια εξαναγκασμένη ταλάντωση ο ταλαντωτής έχει συντονιστεί με το διεγέρτη. Ποιες από τις παρακάτω προτάσεις είναι σωστές; 7. Σύστημα ιδανικό ελατήριο-σώμα εκτελεί εξαναγκασμένη μηχανική ταλάντωση με πολύ μικρή σταθερά απόσβεσης \[b\] και με τη βοήθεια διεγέρτη τροχού. Το σύστημα έχει ιδιοσυχνότητα \[f_0\] και ο διεγέρτης ιδιοσυχνότητα \[f_δ\]. Αρχικά το σύστημα δε βρίσκεται σε συντονισμό. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Για να βρεθεί το σύστημα σε κατάσταση συντονισμού πρέπει: 8. Η χρονοεξίσωση της δυναμικής ενέργειας ταλαντωτή που εκτελεί εξαναγκασμένη μηχανική ταλάντωση σταθερού πλάτους \[A\] είναι \[U_T=\frac{1}{2} mω_1^2 Α^2 ημ^2 (ω_2 t+φ_0)\]. 10. Δύο σώματα Α, Β με ίσες μάζες είναι δεμένα στα άκρα δύο ανεξάρτητων ιδανικών ελατηρίων και εκτελούν φθίνουσες ταλαντώσεις μικρής απόσβεσης με ίδιο αρχικό πλάτος \[Α_0\]. Οι συνισταμένες δυνάμεις για την κάθε ταλάντωση δίνονται απ’ τις σχέσεις \[ΣF_A=-100 x_A-2υ_Α\] (S.I.), \[ΣF_B=-100x_A-4υ_Α\] (S.I.) όπου \[x,\, υ\] οι αλγεβρικές τιμές της απομάκρυνσης και της ταχύτητας αντίστοιχα για τον κάθε ταλαντωτή.Α. Τη χρονική στιγμή \[t=0\]:
α) το σώμα Α έχει μεγαλύτερη ενέργεια ταλάντωσης.
β) το σώμα Β έχει μεγαλύτερη ενέργεια ταλάντωσης.
γ) τα δύο σώματα έχουν ίσες ενέργειες ταλάντωσης.
Β. Για τις συχνότητες των δύο ταλαντωτών ισχύει:
α) \[f_A=f_B\]. β) \[f_A > f_B\]. γ) \[ f_A < f_B\].
Γ. Για τους χρόνους ημιζωής των δύο ταλαντώσεων \[t_{\frac 12 A},\, t_{\frac 12 B}\] ισχύει:
α) \[t_{\frac 12 A}=t_{\frac 12 B}\].
β) \[t_{\frac 12 A} < t_{\frac 12 B} \].
γ) \[t_{\frac 12 A} > t_{\frac 12 B} \].
11. Το σώμα μάζας \[m\] του παρακάτω σχήματος ισορροπεί δεμένο στο κάτω άκρο ιδανικού ελατηρίου σταθεράς \[k\] πάνω σε λείο κεκλιμένο επίπεδο γωνίας κλίσης \[φ\] με \[ημφ=0,6\]. Στη θέση ισορροπίας το ελατήριο είναι επιμηκυμένο κατά \[Δ\ell\]. Την \[t=0\] ασκώ στο σώμα σταθερή δύναμη \[F\] που έχει τη διεύθυνση του άξονα του ελατηρίου με φορά προς τα πάνω και μέτρο \[F=0,3w\] όπου \[w\] το βάρος του σώματος. Το σώμα αρχίζει να εκτελεί α.α.τ. με \[D=k\] χωρίς να καταργήσουμε την \[F\] με θετική φορά πάνω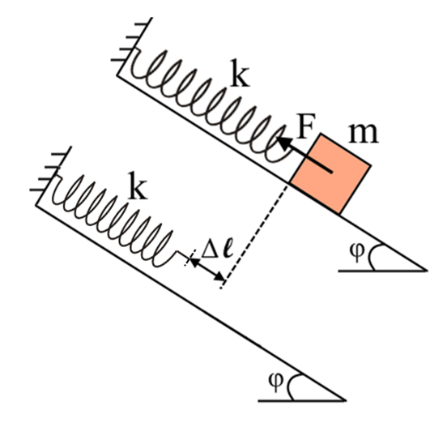
Α) Η ενέργεια της α.α.τ. του σώματος είναι:
α) \[\frac{kΔl^2}{2}\], β) \[\frac{kΔl^2}{4}\], γ) \[\frac{kΔl^2}{8}\].
B) Το σώμα περνά απ’ τη Θ.Φ.Μ. του ελατηρίου για πρώτη φορά την που είναι:
α) \[π\sqrt{ \frac{m}{k} }\],
β) \[\frac{ π}{2} \sqrt{ \frac{m}{k} }\],
γ) \[\frac{π}{6} \sqrt{ \frac{m}{k} } \].
12. Όταν τα αμορτισέρ του αυτοκινήτου παλιώσουν τότε: 13. Απ’ τις πειραματικές μετρήσεις μιας εξαναγκασμένης ταλάντωσης συστήματος ελατηρίου-σώματος που γίνεται με τη βοήθεια διεγέρτη-τροχού προκύπτει το παρακάτω διάγραμμα που δείχνει τη μεταβολή του πλάτους της ταλάντωσης με τη συχνότητα του διεγέρτη. Το πείραμα γίνεται με συγκεκριμένη σταθερά απόσβεσης \[b\]. Ποιες από τις παρακάτω προτάσεις είναι σωστές;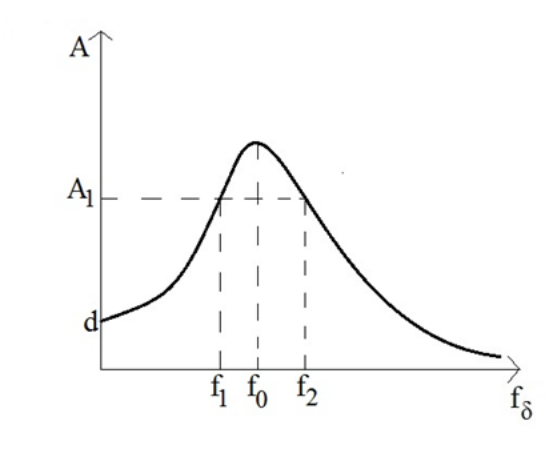
14. Σύστημα ιδανικό ελατήριο-σώμα βρίσκεται σε λείο οριζόντιο επίπεδο και ισορροπεί ακίνητο στη θέση που το ελατήριο έχει το φυσικό του μήκος. Εκτρέπω το σώμα απ’ τη Θ.Ι. του κατά \[x_0\] στη διεύθυνση του άξονα του ελατηρίου και απ’ τη θέση αυτή το αφήνω ελεύθερο να κινηθεί. Το σύστημα εκτελεί α.α.τ. Αν επαναλάβω το ίδιο πείραμα διπλασιάζοντας την αρχική εκτροπή \[x_0\], ποιες από τις παρακάτω προτάσεις είναι σωστές; 15. Σώμα εκτελεί φθίνουσα ταλάντωση και η αντιτιθέμενη δύναμη που δέχεται είναι της μορφής \[ΣF=-bυ\], όπου \[b\] η σταθερά απόσβεσης και \[υ\] η αλγεβρική τιμή της ταχύτητάς του. Ποιες από τις παρακάτω προτάσεις είναι σωστές; 16. Σώμα μάζας \[m\] ισορροπεί ακίνητο στο κάτω άκρο ιδανικού ελατηρίου σταθεράς \[k\] που το άλλο άκρο του είναι ακλόνητα στερεωμένο. Το σύστημα βρίσκεται σε λείο κεκλιμένο επίπεδο γωνίας κλίσης \[φ\]. Στο σώμα ασκείται το βάρος, η δύναμη του ελατηρίου και η κάθετη αντίδραση από το κεκλιμένο επίπεδο. Ανυψώνω το σώμα κατά τη διεύθυνση του κεκλιμένου επιπέδου μέχρι τη θέση που το ελατήριο έχει το φυσικό του μήκος και απ’ τη θέση αυτή το αφήνω την \[t=0\] και αυτό εκτελεί α.α.τ. Ποιες από τις παρακάτω προτάσεις είναι σωστές; 17. Δύο κατακόρυφα ιδανικά ελατήρια με σταθερές \[k_1, k_2\] έχουν τα πάνω άκρα τους στερεωμένα σε οροφή ενώ στα κάτω άκρα δένουμε από ένα σώμα. Τα σώματα έχουν μάζες \[m_1, m_2\] αντίστοιχα με \[m_1 > m_2\] και ισορροπούν ακίνητα. Στις Θ.Ι. των σωμάτων τα ελατήρια έχουν την ίδια επιμήκυνση. Εκτρέπω τα σώματα κατά ίδιο \[x_0\] κατακόρυφα προς τα κάτω και τα αφήνω ταυτόχρονα από εκεί ελεύθερα. Τα σώματα εκτελούν α.α.τ. Επιλέξτε τις σωστές απαντήσεις. 18. Το σύστημα των σωμάτων \[Σ_1\], \[Σ_2\] του διπλανού σχήματος εκτελεί α.α.τ. Το \[Σ_1\] είναι δεμένο στο ιδανικό ελατήριο, ενώ το \[Σ_2\] ακουμπάει πάνω στο \[Σ_1\]. Ποιες από τις επόμενες προτάσεις είναι σωστές;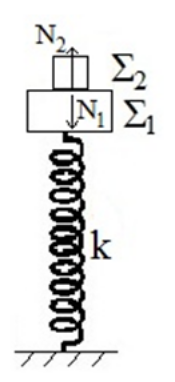
21. Ταλαντωτής έχει μάζα \[m\] και γωνιακή ιδιοσυχνότητα \[ω_0\] και εκτελεί εξαναγκασμένη μηχανική ταλάντωση με μικρή σταθερά απόσβεσης και σταθερού πλάτους \[Α\] με την επίδραση διεγείρουσας δύναμης \[F_δ\] που έχει τη μορφή \[F_δ=F_0 συνω_δ t\]. Η χρονοεξίσωση της δυναμικής ενέργειας της ταλάντωσης για μεγάλους χρόνους \[t\] γράφεται: 24. Ο ταλαντωτής ιδιοσυχνότητας \[f_0\] εκτελεί εξαναγκασμένη μηχανική ταλάντωση πλάτους \[Α\] με σταθερή συχνότητα διεγέρτη \[f_δ ≠ f_0\]. Ποιες από τις επόμενες προτάσεις είναι σωστές; 25. Στο θάλαμο της πειραματικής διάταξης για τη μελέτη μιας φθίνουσας μηχανικής ταλάντωσης διατηρούμε την πίεση του αέρα που περιέχει σταθερή και διεγείρουμε το σύστημα ελατήριο-σώμα ώστε ν’ αρχίσει να ταλαντώνεται προσφέροντάς του την \[t=0\] αρχική ενέργεια \[E_{T,0}\]. Την \[t=0\] ο ταλαντωτής έχει πλάτος \[A_0\]. Ποιες από τις παρακάτω προτάσεις είναι σωστές; 26. Σε μια α.α.τ. με περίοδο \[Τ\] η αρχική φάση είναι \[φ_0=\frac{3π}{2} \; rad\]. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές; 28. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Στο θάλαμο της πειραματικής διάταξης για τη μελέτη της φθίνουσας μηχανικής ταλάντωσης, όταν αυξάνεται η πίεση του αέρα που περιέχεται σ’ αυτόν: 29. Σε μια φθίνουσα μηχανική ταλάντωση περιόδου \[Τ\] το πλάτος της μειώνεται με το χρόνο σύμφωνα με τη σχέση \[Α=Α_0\, e^{-Λt}\] όπου \[Λ\] θετική σταθερά.Α. Να δείξετε ότι το επί τοις εκατό ποσοστό μείωσης του πλάτους στη διάρκεια μιας περιόδου είναι σταθερό και ίσο με:
α) \[π_1=e^{ΛT}⋅100 \% \].
β) \[π_1=e^{-ΛT}⋅100\%\].
γ) \[π_1=\left(1-e^{-ΛT} \right)⋅100\%\].
δ) \[π_1=\left(1-e^{ΛT} \right)⋅100\%\].
Β. Αν το πλάτος της ταλάντωσης τη στιγμή \[t=0\] είναι \[Α_0=5\, cm\] και το παραπάνω ποσοστό είναι \[π_1=10\%\], τότε το πλάτος τη στιγμή \[t_2=2T\] είναι:
α) \[Α_2=4,5\, cm\]. β) \[Α_2=4\, cm\]. γ) \[Α_2=3,5\, cm\]. δ) \[Α_2=4,05\, cm\].
Γ. Η μείωση του πλάτους ανά περίοδο με το πέρασμα του χρόνου
α) αυξάνεται. β) μειώνεται. γ) μένει σταθερή.
