1. Στο παρακάτω σχήμα ο ευθύγραμμος αγωγός ΚΛ μήκους \[\ell\] μπορεί να κινείται χωρίς τριβές με τα άκρα του Κ, Λ να βρίσκονται πάντα σε επαφή με τους οριζόντιους αγωγούς \[Αx_1,\, Γx_2\] που έχουν μεγάλο μήκος και αμελητέα αντίσταση. Το σύστημα των αγωγών βρίσκεται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο έντασης \[B\] που οι δυναμικές γραμμές του είναι συνεχώς κάθετες στον αγωγό. Αρχικά ο αγωγός ΚΛ είναι ακίνητος και την \[t=0\] ασκώ στο μέσο του οριζόντια σταθερή δύναμη κάθετη στη διεύθυνσή του και αυτός αρχίζει να κινείται παράλληλα στους οριζόντιους αγωγούς μέχρι που αποκτά σταθερή οριακή ταχύτητα \[υ_{ορ}\] τη χρονική στιγμή \[t_1\]. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές;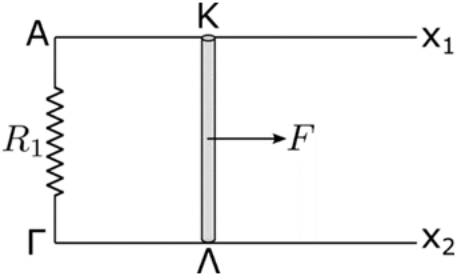
3. Στο παρακάτω σχήμα ο μαγνήτης την \[t=0\] αρχίζει να κινείται στη διεύθυνση κοινού άξονα σωληνοειδούς μαγνήτη πλησιάζοντας το σωληνοειδές και ακινητοποιείται τη στιγμή \[t_1\] που δεν έχει έρθει ακόμα σε επαφή με το άκρο Κ του σωληνοειδούς. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές;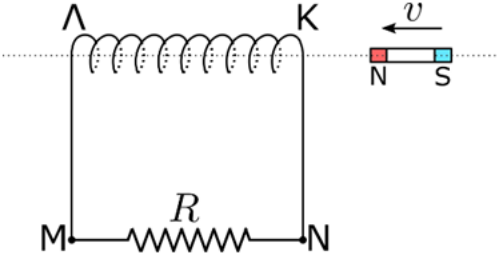
4. Τα παρακάτω πλαίσια \[(1),\, (2)\] του παρακάτω σχήματος εισέρχονται με ταχύτητες μέτρων \[υ_1,\, υ_2\] μέσα στο ίδιο ομογενές μαγνητικό πεδίο για τα οποία ισχύει \[υ_1=2υ_2\]. Τα πλαίσια έχουν πλευρές \[α_1=α\] και \[α_2=2 α\] και οι ταχύτητές τους είναι κάθετες στις δυναμικές γραμμές του πεδίου και τις πλευρές των πλαισίων που πρώτα αυτές εισέρχονται στο πεδίο. Τα πλαίσια αποτελούνται από μια σπείρα και είναι ομογενή απ’ το ίδιο ομογενές και ισοπαχές σύρμα. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή;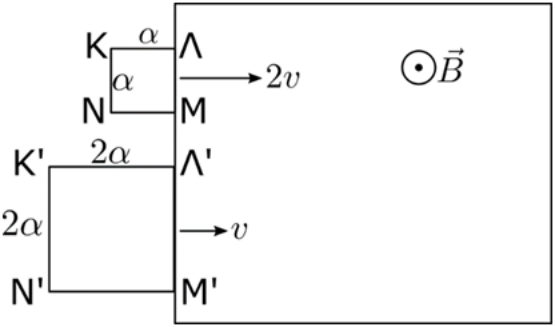
6. Στο παρακάτω σχήμα οι λαμπτήρες \[Λ_1\, , \, Λ_2\] είναι όμοιοι και το πηνίο είναι ιδανικό. Την \[t_0=0\] κλείνουμε το διακόπτη \[δ\]. Ποιες από τις παρακάτω προτάσεις είναι σωστές;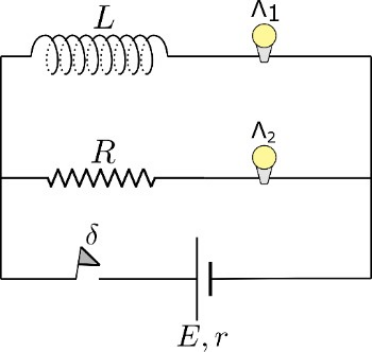
8. Ο ευθύγραμμος αγωγός του παρακάτω σχήματος έχει μήκος \[\ell \] και αντίσταση \[R\] και μπορεί να κινείται χωρίς τριβές έχοντας στα άκρα του συνεχώς σε επαφή με τους λείους ευθύγραμμους παράλληλους λείους αγωγούς \[Αx\] και \[Γy\] που έχουν μεγάλο μήκος και αμελητέα αντίσταση. Το επίπεδο των δύο αγωγών βρίσκεται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο που οι δυναμικές γραμμές του είναι κάθετες στο επίπεδο των αγωγών. Αρχικά ο αγωγός είναι ακίνητος. Ασκούμε στο κέντρο του οριζόντια σταθερή δύναμη μέτρου \[F\] κάθετη στη διεύθυνσή του και αυτός αρχίζει να κινείται παράλληλα στους αγωγούς \[Αx\] και \[Γy\] με τα άκρα του να μένουν πάντα σ’ επαφή με αυτόν. Ποιες από τις παρακάτω προτάσεις είναι σωστές;
9. Στο παρακάτω σχήμα τα δύο πηνία \[Π_1,\, Π_2\] έχουν κοινό άξονα και βρίσκονται σε μικρή μεταξύ τους απόσταση. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές;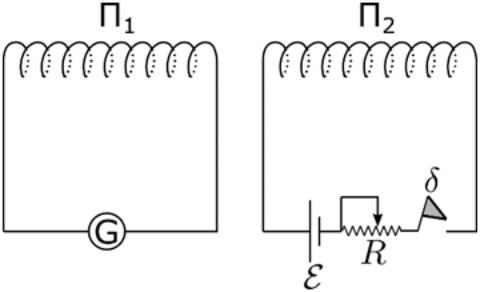
10. Ένας κυκλικός αγωγός δένεται σε οροφή μέσω μονωτικού νήματος ώστε το επίπεδό του να διατηρείται κατακόρυφο. Ένας οριζόντιος ραβδόμορφος μαγνήτης έχει άξονα που διέρχεται απ’ το κέντρο του κυκλικού αγωγού και είναι κάθετος στο επίπεδό του όπως φαίνεται στο παρακάτω σχήμα. Πλησιάζουμε τον μαγνήτη προς τον αγωγό κατά τη διεύθυνση του άξονα του μαγνήτη. Ποιες απ’ τις επόμενες προτάσεις είναι σωστές;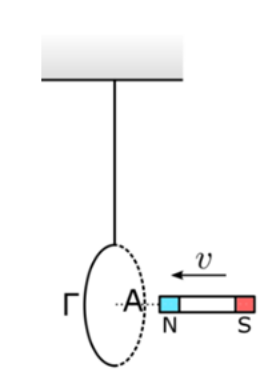
11. Στα άκρα αντιστάτη αντίστασης \[R=10\, Ω\] εφαρμόζουμε εναλλασσόμενη τάση με εξίσωση \[v=20\sqrt{2}\, ημ100πt\] (S.I.). Ποιες από τις παρακάτω προτάσεις είναι σωστές; 12. Στη διάταξη του παρακάτω σχήματος οι οριζόντιοι λείοι αγωγοί \[Αx\] και \[Γy\] είναι παράλληλοι, έχουν αμελητέα αντίσταση και τα άκρα τους Α, Γ συνδέονται με αντιστάτη \[R_1=2R\]. Ο οριζόντιος αγωγός ΚΛ είναι κάθετος στους δύο αγωγούς, έχει αντίσταση \[R\], μήκος \[\ell\] και τα άκρα του βρίσκονται σε επαφή με αυτούς. Αρχικά ο αγωγός ΚΛ είναι ακίνητος. Το σύστημα των αγωγών βρίσκεται σε κατακόρυφο ομογενές μαγνητικό πεδίο έντασης μέτρου \[Β\] που οι δυναμικές γραμμές του είναι κάθετες στο επίπεδο των αγωγών. Την \[t=0\] δίνουμε στον αγωγό ΚΛ οριζόντια αρχική ταχύτητα μέτρου \[υ_0\] παράλληλη στους δύο αγωγούς ενώ ταυτόχρονα ασκούμε στο μέσο σταθερή δύναμη μέτρου \[F\] και κατεύθυνσης ομόρροπης της \[υ_0\].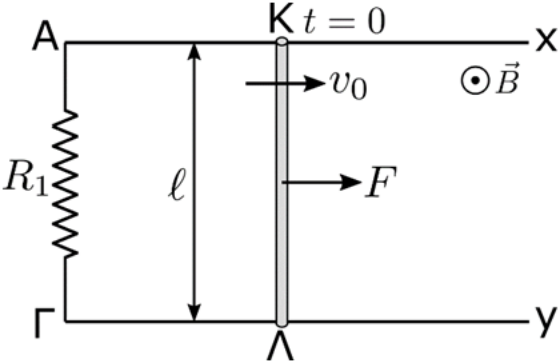
A) Αν το μέτρο της \[υ_0\] είναι \[υ_0 > \frac{ 3FR }{ B^2 \ell^2 }\], τότε ο αγωγός ΚΛ μετά την \[t=0\]:
α) θα εκτελέσει ομαλά επιβραδυνόμενη κίνηση μέχρι να αποκτήσει σταθερή ταχύτητα μέτρου \[υ_1 < υ_0\].
β) θα εκτελέσει επιταχυνόμενη κίνηση (μη ομαλά) μέχρι να αποκτήσει σταθερή ταχύτητα μέτρου \[υ_1 > υ_0\].
γ) θα εκτελέσει επιβραδυνόμενη κίνηση (μη ομαλά) μέχρι να αποκτήσει ταχύτητα μέτρου \[ υ_1 < υ_0 \].
δ) θα εκτελέσει Ε.Ο.Κ. με ταχύτητα \[υ_0\].
B) Απ’ τη στιγμή \[t=0\] ως τη στιγμή \[t_1\] που ο αγωγός ΚΛ έχει σταθερή ταχύτητα \[\vec{υ}_1\], το έργο της δύναμης \[F\]:
α) έχει γίνει αύξηση της κινητικής του αγωγού.
β) είναι ίση με τη συνολική θερμότητα που εκλύεται στους αντιστάτες μέχρι τη στιγμή \[t_1\].
γ) και η μείωση της κινητικής του ενέργειας του αγωγού ΚΛ μέχρι τη στιγμή \[t_1\] μας δίνουν μαζί την θερμότητα που εκλύεται συνολικά στους αντιστάτες μέχρι τη στιγμή \[t_1\].
13. Ένα πηνίο με συντελεστή αυτεπαγωγής \[L=2\, mH\] διαρρέεται από ρεύμα μεταβλητής έντασης όπως απεικονίζεται στο σχήμα. Το πηνίο αποτελείται από \[1000\] σπείρες. Ο ρυθμός μεταβολής της ροής που διέρχεται από την κάθε σπείρα του πηνίου είναι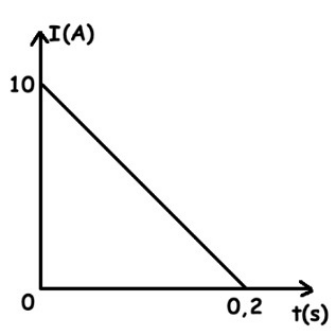
14. Το τετράγωνο πλαίσιο του παρακάτω σχήματος έχει πλευρά μήκους \[α\], αποτελείται από \[N\] σπείρες που η καθεμιά έχει αντίσταση \[R\] και βρίσκεται ακλόνητο πάνω σε οριζόντιο δάπεδο. Το πλαίσιο βρίσκεται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο έντασης \[B_1\] που η κατεύθυνσή του φαίνεται στο παρακάτω σχήμα. Τα άκρα Κ, Λ του πλαισίου συνδέονται μέσω συρμάτων αμελητέας αντίστασης με ευθύγραμμο αγωγό ΑΓ. Ο αγωγός ΑΓ βρίσκεται ακλόνητος στο ίδιο οριζόντιο δάπεδο και έχει αντίσταση \[R\]. Η ένταση \[Β_1\] την \[t=0\] αρχίζει να μεταβάλλει το μέτρο της και η απόλυτη τιμή του ρυθμού μεταβολής \[ \left| \frac{ΔB_1}{Δt } \right| \] είναι σταθερή και ίση με \[λ\]. Στη διάρκεια της μεταβολής αυτής γύρω απ’ τον αγωγό ΑΓ δημιουργείται μαγνητικό πεδίο. Σε σημείο Δ που απέχει \[r\] απ’ τον ευθύγραμμο αγωγό η ένταση του μαγνητικού πεδίου είναι σταθερή, έχει μέτρο \[Β_Δ\] και η φορά της φαίνεται στο σχήμα. Η απόσταση \[r\] είναι πολύ μικρή σε σχέση με το μήκος του αγωγού. H μαγνητική διαπερατότητα του κενού είναι \[μ_0\].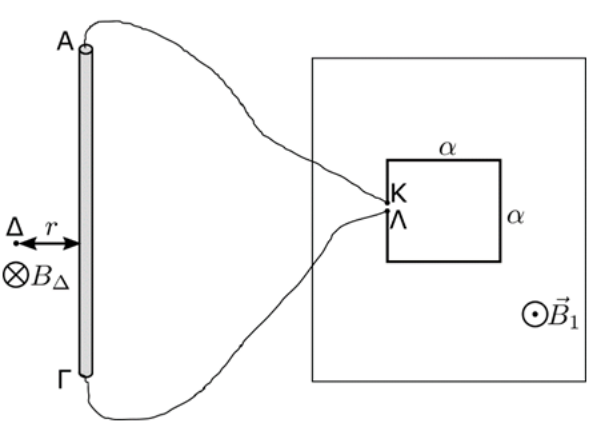
A) Η ένταση του μαγνητικού πεδίου \[B_1\]:
α) αυξάνεται,
β) μειώνεται,
γ) δεν μπορούμε να προβλέψουμε αν αυξάνεται ή μειώνεται.
Β) Η απόλυτη τιμή του ρυθμού μεταβολής του μέτρου της έντασης \[B_1\] είναι:
α) \[λ=\frac{2πΒ_Δ R}{μ_0 α^2 } r\],
β) \[ λ =\frac{2πΒ_Δ (Ν+1)R}{Nμ_0 α^2} r\],
γ) \[λ=\frac{4πΒ_Δ (Ν+1)R}{μ_0 α^2 } r\].
16. Ο ευθύγραμμος αγωγός ΚΛ του παρακάτω σχήματος έχει τα άκρα του σε επαφή και είναι κάθετος με τους λείους κατακόρυφους παράλληλους ευθύγραμμους \[Αy_1\] και \[Γy_2\] που είναι μεγάλου μήκους και αμελητέας αντίστασης. Το σύστημα των τριών αγωγών βρίσκεται σε οριζόντιο ομογενές μαγνητικό πεδίο έντασης \[\vec{B}\] που οι δυναμικές του γραμμές είναι κάθετες στο επίπεδο που δημιουργούν οι τρεις αγωγοί. Την \[t=0\] δίνουμε μια αρχική ταχύτητα \[υ_0\] κατακόρυφη προς τα πάνω και ο αγωγός αρχίζει να ανέρχεται κατακόρυφα και τα άκρα του διατηρούνται σε επαφή με τους κατακόρυφους αγωγούς. Τη χρονική στιγμή \[t_1\] ο αγωγός ακινητοποιείται στιγμιαία και κατόπιν αρχίζει να κατέρχεται κατακόρυφα με τον ίδιο τρόπο. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές;
17. Στο παρακάτω κύκλωμα το πηνίο έχει αντίσταση \[R_π\], ο αντιστάτης αντίσταση \[R\] και η πηγή έχει ΗΕΔ \[Ε\] και εσωτερική αντίσταση \[r\]. Ισχύει ότι \[r=R_π=R\]. Την \[t_0=0\] κλείνουμε το διακόπτη \[δ\] και η ένταση του ρεύματος αρχίζει να αυξάνεται μέχρι να πάρει τη σταθερή τιμή \[I\]. Τη στιγμή που το ρεύμα έχει ένταση \[\frac{I}{2}\], τότε η ΗΕΔ από αυτεπαγωγή στο πηνίο: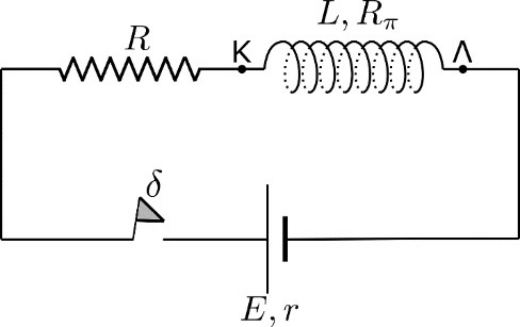
19. Ο ευθύγραμμος οριζόντιος αγωγός ΑΓ έχει αμελητέο βάρος και είναι φτιαγμένος από ομογενές και ισοπαχές σύρμα ειδικής αντίστασης ρ, εμβαδό διατομής \[S\] και μήκος \[\ell\]. Ο αγωγός ΑΓ είναι σε επαφή με λείους κατακόρυφους αγωγούς \[yy'\] και \[y_1 y_1'\] αμελητέας αντίστασης που τα άκρα τους συνδέονται με πλαίσιο τετραγωνικού σχήματος πλευράς \[α\] και \[Ν\] σπειρών που η συνολική του αντίσταση είναι ίση με την αντίσταση του ευθύγραμμου αγωγού ΑΓ. Ο αγωγός ΑΓ βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο σταθερής έντασης \[\vec{B}_2\] που η κατεύθυνσή του φαίνεται στο παρακάτω σχήμα. Ο αγωγός ΑΓ είναι προσδεμένος στο κέντρο από το άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς \[k\] που το άλλο άκρο του είναι στερεωμένο σε οροφή. Το πλαίσιο βρίσκεται μέσα σε άλλο ομογενές μαγνητικό πεδίο έντασης \[\vec{B}_1\] και διατηρείται ακλόνητος με το επίπεδό του κατακόρυφο. Αυξάνουμε με σταθερό ρυθμό \[ \frac{ΔΒ_1} {Δt} = λ\] το μέτρο της έντασης \[Β_1\] χωρίς να μεταβάλλουμε τη φορά της και παρατηρούμε ότι ο αγωγός ΑΓ ισορροπεί με το ελατήριο να είναι παραμορφωμένο κατά \[Δ\ell_1\].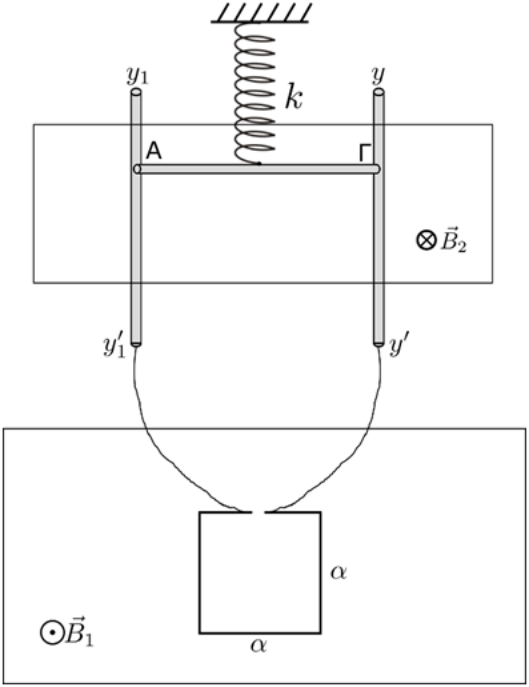
Α) Στη διάρκεια της ισορροπίας του αγωγού ΑΓ:
α) το ελατήριο είναι συσπειρωμένο κατά \[Δ \ell_1=N \frac{ B_2 α^2 λS}{2ρk}\],
β) το ελατήριο είναι επιμηκυμένο κατά \[Δ \ell_1=N \frac{ Β_2 α^2 λS }{ 2ρk } \],
γ) το ελατήριο είναι επιμηκυμένο κατά \[ Δ \ell_1=N \frac{ B_2 α^2 λS }{ ρk } \],
δ) το ελατήριο είναι συσπειρωμένο κατά \[Δ \ell_1=N \frac{ B_2 α^2 λS }{ ρk } \].
B) Αντιστρέφουμε τη φορά της \[\vec{B}_1\] την \[t=0\] που αυτή έχει μέτρο \[B_0\] και αρχίζουμε να μεταβάλλουμε το μέτρο της σύμφωνα με τη σχέση \[B=B_0+2λt\] και τότε ο αγωγός ΑΓ ισορροπεί σε μια νέα θέση που το ελατήριο είναι παραμορφωμένο κατά \[Δ\ell_2\]. Η παραμόρφωση \[Δ \ell_2\] του ελατηρίου είναι:
α) επιμήκυνση και ισχύει \[Δ \ell_2=\frac{ Δ \ell_1}{2}\].
β) συσπείρωση και ισχύει \[Δ \ell_2=\frac{Δ\ell_1}{2} \].
γ) συσπείρωση και ισχύει \[ Δ \ell_2=2Δ \ell_1\].
δ) επιμήκυνση και ισχύει \[Δ \ell_2=2Δ \ell_1\].
21. Ο αγωγός ΚΛ του παρακάτω σχήματος έχει μήκος \[\ell\] και κατέρχεται με σταθερή ταχύτητα μέτρου \[υ\] έχοντας τα άκρα του Κ, Λ σε επαφή με τους λείους ευθύγραμμους κατακόρυφους αγωγούς \[Αy_1\] και \[Γy_2\] παραμένοντας συνεχώς κάθετος σ’ αυτούς. Το σύστημα των αγωγών βρίσκεται σε οριζόντιο μαγνητικό πεδίο έντασης \[\vec{B}\] που οι δυναμικές γραμμές του είναι κάθετες στο επίπεδο των αγωγών. Ποιες από τις παρακάτω προτάσεις είναι σωστές;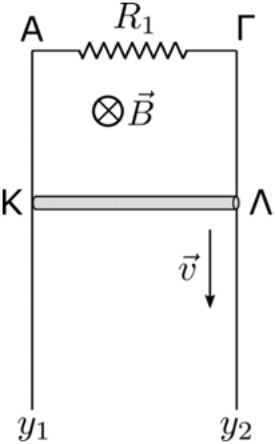
22. Στο παρακάτω κύκλωμα το πηνίο είναι ιδανικό και οι λαμπτήρες είναι όμοιοι. Ο διακόπτης \[δ\] είναι κλειστός και η ενέργεια του μαγνητικού πεδίου του πηνίου έχει σταθερή τιμή. Την \[t=0\] ανοίγουμε τον \[δ\] χωρίς να δημιουργηθεί σπινθήρας. Ποιες από τις επόμενες προτάσεις είναι σωστές;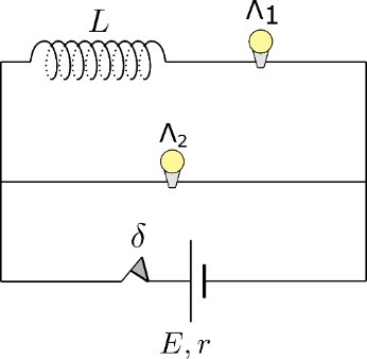
24. Ο ευθύγραμμος αγωγός ΚΛ του παρακάτω σχήματος έχει τα άκρα του σε επαφή με δύο παράλληλους ευθύγραμμους οριζόντιους αγωγούς \[Αx_1\] και \[Γx_2\] που έχουν μεγάλο μήκος και αμελητέα αντίσταση. Την \[t=0\] ο αγωγός έχει αρχική ταχύτητα μέτρου \[υ_0\] παράλληλη στους δύο άλλους αγωγούς. Τη στιγμή αυτή ασκώ στον αγωγό σταθερή δύναμη \[F\] ομόρροπη της ταχύτητας. Το σύστημα των αγωγών βρίσκεται σε κατακόρυφο ομογενές μαγνητικό πεδίο έντασης \[Β\] που οι δυναμικές γραμμές είναι κάθετες στο επίπεδο των αγωγών. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές;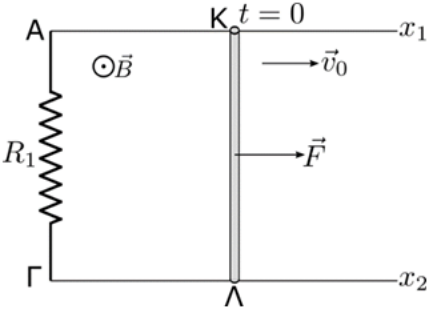
26. Ο δίσκος του Faraday ακτίνας \[r\] στο παρακάτω σχήμα στρέφεται με σταθερή γωνιακή ταχύτητα γύρω από άξονα \[xx'\] που περνά απ’ το κέντρο του και είναι κάθετο στο επίπεδό του. Δύο ολισθαίνουσες επαφές (ψήκτρες) έχουν τοποθετηθεί όπως φαίνεται στο σχήμα. Ποιες από τις παρακάτω προτάσεις είναι σωστές;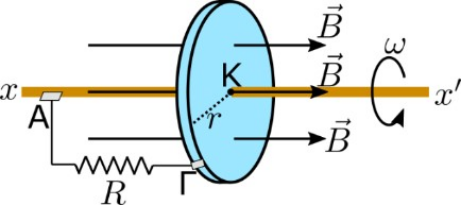
28. Η οριζόντια ράβδος ΟΓ έχει μήκος \[\ell\], αντίσταση \[2R\] και στρέφεται με σταθερή γωνιακή ταχύτητα σε οριζόντιο επίπεδο γύρω από κατακόρυφο άξονα που διέρχεται απ’ το άκρο της Ο. Το μέσο Μ της ράβδου βρίσκεται σε επαφή με κυκλικό αγωγό κέντρου Ο και ακτίνας \[\frac{\ell }{2 }\] που το επίπεδό του ταυτίζεται με το επίπεδο περιστροφής της ράβδου. Μεταξύ του σημείου Ο και του σημείου Κ του αγωγού συνδέουμε αντιστάτη αντίστασης \[R\]. Το σύστημα των αγωγών βρίσκεται σε κατακόρυφο ομογενές μαγνητικό πεδίο έντασης μέτρου \[Β\]. Ο ρυθμός εκτέλεσης έργου της δύναμης Laplace (η ισχύς της) είναι: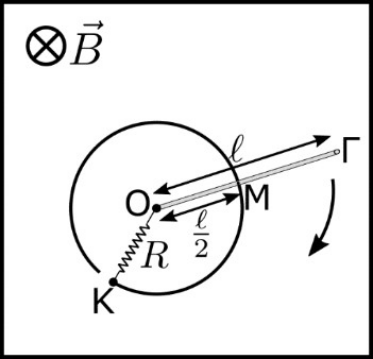
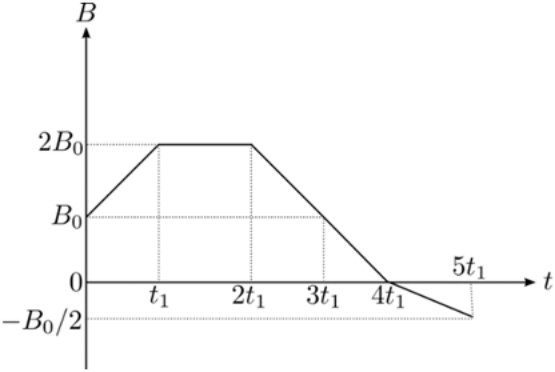
29. Κλειστό συρμάτινο πλαίσιο αντίστασης \[R\] βρίσκεται εντός ομογενούς μαγνητικού πεδίου με το επίπεδό του κάθετο στις δυναμικές γραμμές του. Η μεταβολή της αλγεβρικής τιμής της έντασης \[B\] του μαγνητικού πεδίου φαίνεται στο παρακάτω διάγραμμα. Το πλαίσιο έχει σχήμα τετραγώνου πλευράς \[α\] και αποτελείται από \[N\] όμοιες σπείρες. Ποιες απ’ τις επόμενες προτάσεις είναι σωστές;