2. Φορτισμένο σωματίδιο μάζας \[m\] και φορτίου \[q\] εισέρχεται σε ομογενές μαγνητικό πεδίο έντασης \[\vec{B}\] με ταχύτητα \[\vec{υ}\] που σχηματίζει γωνία \[φ=60^0\] με τις δυναμικές γραμμές του πεδίου. Το σωματίδιο εκτελεί ελικοειδή κίνηση και η μόνη δύναμη που δέχεται είναι αυτή απ’ το μαγνητικό πεδίο. Ποιες απ’ τις επόμενες προτάσεις είναι σωστές; 3. Δύο φορτισμένα σωματίδια (1), (2) έχουν ίσες κατά μέτρο ορμές, μάζες \[m_1=2m_2\] και ίσα φορτία. Τα σωματίδια εισέρχονται στο ίδιο ομογενές μαγνητικό πεδίο και εκτελούν σ’ αυτό ομαλή κυκλική κίνηση με ακτίνες \[R_1, R_2\] και περιόδων \[T_1, T_2\] αντίστοιχα με την επίδραση μόνο της δύναμης Lorentz που δέχονται απ’ το πεδίο. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή; Για τις ακτίνες και τις περιόδους των κυκλικών κινήσεων των δύο σωματιδίων ισχύει: 5. Το πλαίσιο ΚΛΜΝ με πλευρές \[α,\, γ\] του παρακάτω σχήματος είναι προσδεμένο απ’ το μέσο της πλευράς του ΚΛ απ’ το άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς \[k\] που το άλλο άκρο του είναι προσδεμένο σε οροφή. Το πλαίσιο διαρρέεται από ρεύμα έντασης \[I\] που η φορά του φαίνεται στο σχήμα ενώ βρίσκεται κατά ένα μέρος του (κάτω απ’ την ευθεία ε) μέσα σε οριζόντιο ομογενές μαγνητικό πεδίο έντασης μέτρου \[B_1\] με φορά προς τον αναγνώστη, ενώ το υπόλοιπο είναι εκτός πεδίου (σχ. α). Το πλαίσιο ισορροπεί ακίνητο και το ελατήριο είναι επιμηκυμένο κατά \[Δ\ell\]. Δημιουργούμε δεύτερο οριζόντιο ομογενές μαγνητικό πεδίο έντασης μέτρου \[B_2\] αντίρροπης της \[B_1\]. Το πεδίο έντασης \[Β_2\] αυτό εκτείνεται πάνω απ’ την ευθεία ε (σχ. β). Τώρα το πλαίσιο ισορροπεί με το ελατήριο να είναι παραμορφωμένο κατά \[1,5Δ\ell\]. Το βάρος του πλαισίου έχει μέτρο \[w=\frac{ B_1 I α }{ 2 } \].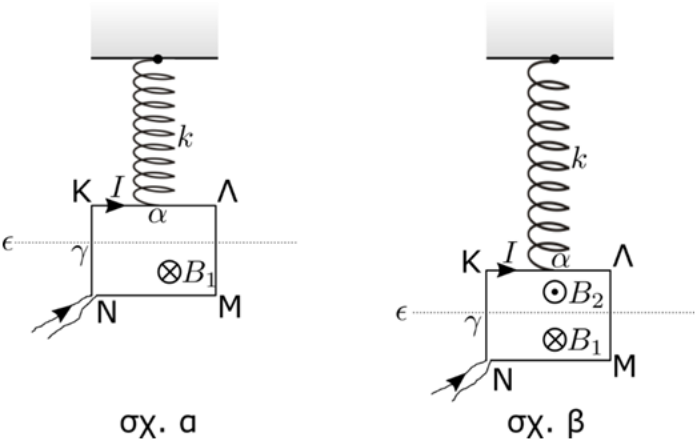
Α) Για τα μέτρα των εντάσεων των δύο μαγνητικών πεδίων ισχύει:
α) \[B_1=\frac{4}{3} B_2\],
β) \[B_1=\frac{3}{2} B_2\],
γ) \[Β_1=\frac{Β_2}{2}\].
Β) Αν αντιστρέψω τη φορά της έντασης \[Β_2\], τότε το πλαίσιο θα ισορροπεί όταν το ελατήριο έχει επιμήκυνση \[Δ \ell'\] που είναι ίση με:
α) \[Δ \ell \], β) \[0,75\, Δ\ell \], γ) \[0,5\, Δ\ell\].
6. Ο αγωγός του παρακάτω σχήματος ισορροπεί οριζόντιος μέσα σε οριζόντιο ομογενές μαγνητικό πεδίο έντασης \[\vec{B}\]. Ο αγωγός ακουμπά χωρίς τριβές σε δύο αγώγιμες κατακόρυφες ράβδους που στα άκρα τους έχουμε συνδέσει ηλεκτρική πηγή. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές;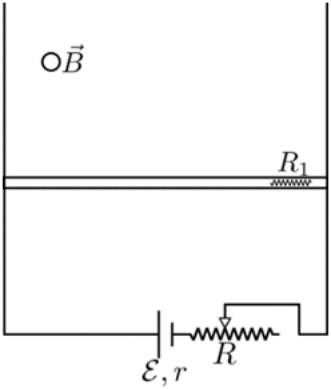
8. Ποιες απ’ τις επόμενες προτάσεις είναι σωστές; Με το φασματογράφο μάζας: 9. Στο παρακάτω σχήμα φαίνονται δύο κλειστές διαδρομές \[S_1\, , \, S_2\] σχήματος ομοεπίπεδων τετραγώνων πλευράς \[α\, ,\, 2α\] αντίστοιχα και οι φορές διαγραφής. Η διαδρομή \[S_1\] περικλείει τρεις ευθύγραμμους παράλληλους αγωγούς που διαρρέονται από ομόρροπα ρεύματα ίδιας έντασης \[Ι\] το καθένα. Η διεύθυνση των αγωγών είναι κάθετη στο επίπεδο των δύο επιφανειών. Για να γίνει το άθροισμα \[∑B\cdot Δ\ell \cdot συνφ\] στη διαδρομή \[S_2\] ίσο με το μηδέν χωρίς ν’ αλλάξει το αντίστοιχο άθροισμα στη διαδρομή \[S_1\] πρέπει: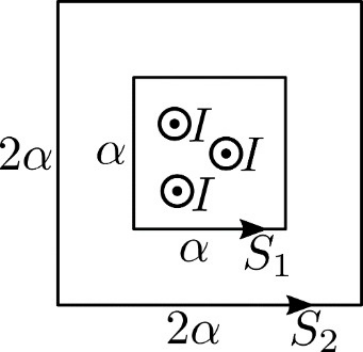
11. Στο παρακάτω σχήμα φαίνονται οι τροχιές δύο ισότοπων ιόντων ίδιου φορτίου \[(1)\] και \[(2)\] του στοιχείου νέου \[(Ne)\] μιας δέσμης ισότοπων του στοιχείου αυτού που εισέρχονται στο μαγνητικό πεδίο έντασης \[\vec{B} '\] ενός φασματογράφου μάζας. Το ιόν \[(1)\] είναι ισότοπο του \[^{20} Ne\] και το ιόν \[(2)\] του \[^{22}Ne\]. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή;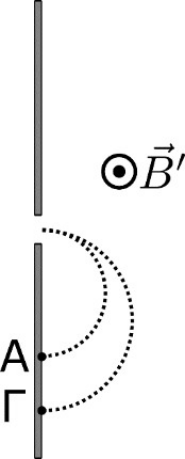
17. Ένα πρωτόνιο μάζας \[m_p\] και φορτίου \[e\] (στοιχειώδες φορτίο) και ένας πυρήνας ηλίου μάζας \[4m_p\] και φορτίου \[2e\] εκτελούν κυκλικές τροχιές με ακτίνες \[R_p\, , \, R_α\] αντίστοιχα με ίσες κατά μέτρο ταχύτητες. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές;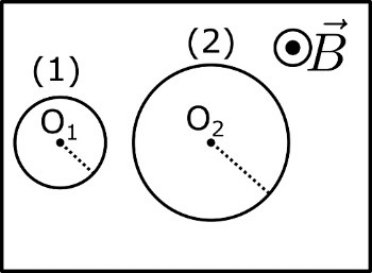
18. Ένα πρωτόνιο \[p\] μάζας \[m_p\] και φορτίου \[e\] και ένα σωμάτιο \[α\] μάζας \[m_α=4m_p\] και φορτίου \[q_α=2e\] όπου \[e\] το στοιχειώδες θετικό φορτίο εισέρχονται ταυτόχρονα απ’ το ίδιο σημείο Γ με ταχύτητες \[\vec{υ}_α\, , \, \vec{υ}_p \] σε ομογενές μαγνητικό πεδίο έντασης \[\vec{Β}\] έτσι ώστε οι ταχύτητές τους να είναι κάθετες στις δυναμικές γραμμές του πεδίου και στο όριό του που είναι η ευθεία \[xx'\] όπως φαίνεται στο παρακάτω σχήμα. Τα σωματίδια δέχονται μόνο τις δυνάμεις απ’ το μαγνητικό πεδίο που εκτείνεται σε μεγάλη απόσταση πάνω απ’ το όριο του \[xx'\]. Κατά την είσοδό τους στο πεδίο έχουν ίσες κινητικές ενέργειες \[(K_p=K_α )\]. Για τα μέτρα των ρυθμών μεταβολής της ορμής των δύο σωματιδίων κατά την παραμονή τους στο μαγνητικό πεδίο ισχύει: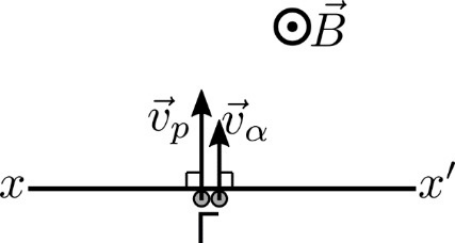
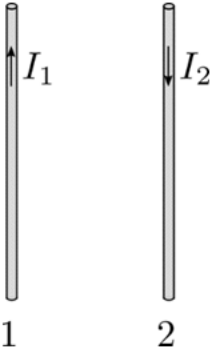
19. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή; Η ένταση \[\vec{Β}\] που υπολογίζουμε απ’ το νόμο του Ampere: \[∑B\cdot Δ\ell \cdot συνθ=μ_0 Ι_{εγκ}\] οφείλεται: 21. Σωματίδιο μάζας \[m\] και φορτίου \[q\] εισέρχεται σε ομογενές μαγνητικό πεδίο έντασης \[\vec{B}\] με ταχύτητα \[\vec{υ}\] που σχηματίζει γωνία \[φ = 30^0 \] με τις δυναμικές γραμμές του. Το σωματίδιο εκτελεί ελικοειδή κίνηση και η μόνη δύναμη που δέχεται είναι αυτή του μαγνητικού πεδίου. Ποιες από τις παρακάτω προτάσεις είναι σωστές; 24. Οι δύο παράλληλοι ρευματοφόροι αγωγοί \[(1),\, (2)\] του παρακάτω σχήματος βρίσκονται ακλόνητοι πάνω σε λείο οριζόντιο μονωτικό επίπεδο και διαρρέονται από αντίρροπα ρεύματα \[Ι_1,\, Ι_2\] αντίστοιχα με \[I_1 < I_2\]. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή; Η θέση που μπορώ να τοποθετήσω έναν τρίτο παράλληλο ρευματοφόρο αγωγό \[(3)\] ώστε αυτός να ισορροπεί είναι: