5. Η σφαιρική επιφάνεια του παρακάτω σχήματος είναι τοποθετημένη μέσα σε μαγνητικό πεδίο. Ποια απ’ τις επόμενες προτάσεις είναι σωστή;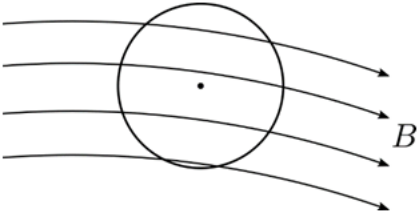
7. Το μεταλλικό οριζόντιο πλαίσιο ΚΛΜΝ βρίσκεται κατά ένα μέρος μέσα σε ομογενές κατακόρυφο μαγνητικό πεδίο έντασης \[\vec{B}\]. Το μέσο Ο της πλευράς ΛΜ είναι το κέντρο οριζόντιου ορθογώνιου συστήματος αξόνων \[xOy\] που ο άξονας του \[y' y\] ταυτίζεται με την πλευρά ΛΜ όπως φαίνεται στο σχήμα. Το μαγνητικό πεδίο εκτείνεται μόνο στο δεύτερο τεταρτημόριο που δημιουργεί το σύστημα των αξόνων \[xOy\].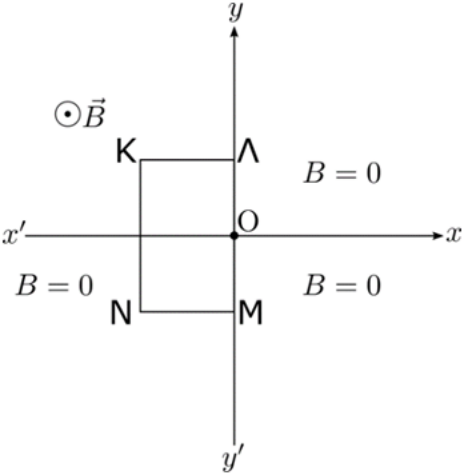
A) Στο πλαίσιο δημιουργείται επαγωγική ΗΕΔ:
α) όταν παραμένει ακίνητο.
β) όταν αρχίζει να κινείται κατά τη θετική φορά του άξονα \[x' x\].
γ) όταν αρχίζει να κινείται κατά την αρνητική φορά του άξονα \[x' x\].
Β) Αν το πλαίσιο αρχίζει να κινείται κατά την αρνητική φορά του άξονα \[y' y\] τότε το πλαίσιο:
α) αρχίζει να διαρρέεται από επαγωγικό ρεύμα που έχει την αντιωρολογιακή φορά.
β) αρχίζει να διαρρέεται από επαγωγικό ρεύμα που έχει την ωρολογιακή φορά.
γ) δεν διαρρέεται από επαγωγικό ρεύμα.
13. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή; Αν σε ένα μαγνητικό πεδίο τοποθετήσω μια κλειστή επιφάνεια, τότε η μαγνητική ροή που διέρχεται απ’ την επιφάνεια αυτή είναι \[0\] γιατί: 17. Η ράβδος ΟΓ του παρακάτω σχήματος έχει μήκος \[ \ell \] και αποτελείται από δύο ίσα τμήματα. Το ένα τμήμα ΟΑ είναι από πλαστικό και το άλλο τμήμα ΑΓ είναι από μέταλλο. Η ράβδος στρέφεται με σταθερή γωνιακή ταχύτητα μέτρου \[ω\] ως προς άξονα κάθετο σ’ αυτήν, που διέρχεται απ’ το άκρο της Ο. Η ράβδος βρίσκεται σε ομογενές μαγνητικό πεδίο έντασης μέτρου \[Β\] που οι γραμμές του είναι παράλληλες στον άξονα περιστροφής. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή; Η επαγωγική ΗΕΔ που εμφανίζεται στο τμήμα ΑΓ της ράβδου είναι ίση με: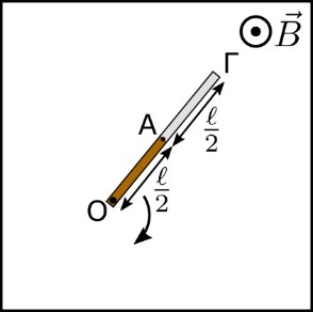
19. Στο παρακάτω σχήμα ο οριζόντιος άξονας του ραβδόμορφου μαγνήτη περνά απ’ το κέντρο του κυκλικού αγωγού που σ’ αυτόν έχει δημιουργηθεί εγκοπή. Ποια απ’ τις επόμενες προτάσεις είναι σωστή; Αν ο μαγνήτης αρχίζει να κινείται προς τα δεξιά: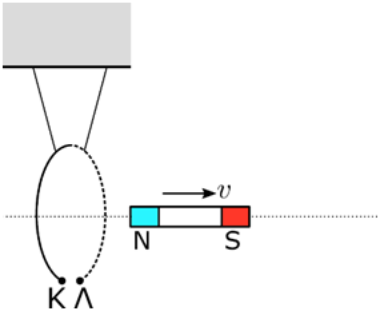
22. Οι οριζόντιοι ευθύγραμμοι αγωγοί ΟΓ και ΟΑ έχουν μήκη \[\ell\] και \[\frac{\ell }{ 2 }\] αντίστοιχα και στρέφονται στο ίδιο οριζόντιο επίπεδο με ίδια σταθερή γωνιακή ταχύτητα μέτρου \[ω\] γύρω από κατακόρυφο άξονα που διέρχεται απ’ το κοινό τους άκρο Ο. Το σύστημα των δύο αγωγών βρίσκεται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο έντασης μέτρου \[Β\]. Η διαφορά δυναμικού \[V_{ΓΑ}\] μεταξύ των σημείων Γ, Α είναι ίση με: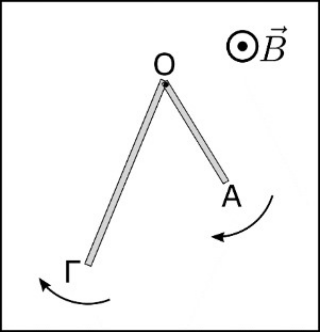
29. Η αγώγιμη ράβδος ΟΑ μήκους \[\ell\] στρέφεται γύρω από άξονα που διέρχεται απ’ το Ο και είναι κάθετη σ’ αυτήν με σταθερή γωνιακή ταχύτητα \[ω\]. Η ράβδος βρίσκεται σε ομογενές μαγνητικό πεδίο έντασης \[Β\] που οι δυναμικές γραμμές του είναι παράλληλες στον άξονα περιστροφής της. Ποιες από τις παρακάτω προτάσεις είναι σωστές;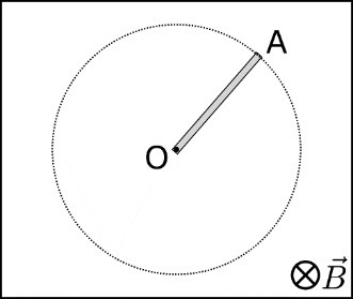
30. Ο ανοικτός μεταλλικός δακτύλιος του παρακάτω σχήματος διατηρείται ακλόνητος. Ο ραβδόμορφος μαγνήτης πλησιάζει τον δακτύλιο με σταθερή ταχύτητα \[υ\].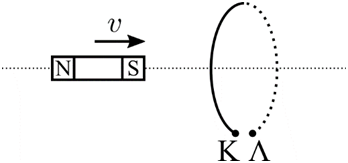
Α) Στη διάρκεια του πλησιάσματος :
α) ο δακτύλιος αποκτά βόρειο και νότιο πόλο.
β) ο δακτύλιος διαρρέεται από επαγωγικό ρεύμα.
γ) προσφέρουμε συνεχώς ενέργεια στο μαγνήτη.
δ) ο δακτύλιος αποκτά επαγωγική ΗΕΔ.
Β) Στη διάρκεια του πλησιάσματος του μαγνήτη:
α) στα άκρα του δακτυλίου δημιουργείται επαγωγική τάση με (+) στο άκρο Κ.
β) στα άκρα του δακτυλίου δημιουργείται επαγωγική τάση με (+) στο άκρο Λ.
γ) στο δακτύλιο δεν εμφανίζεται επαγωγική τάση.
