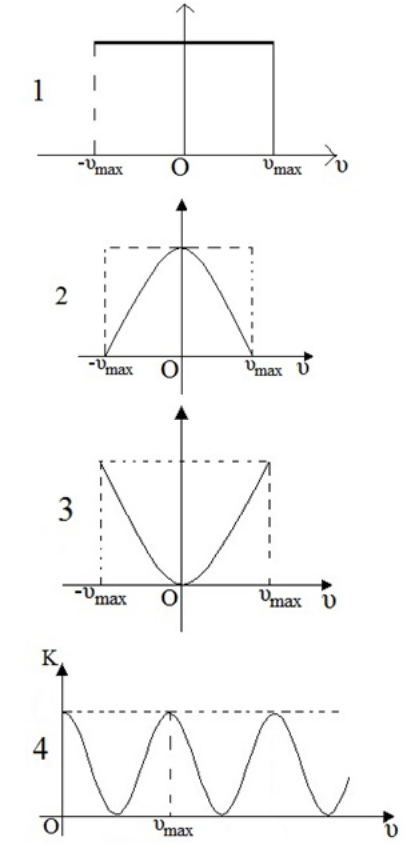
1. Στη θέση ισορροπίας μιας α.α.τ.: 3. Υλικό σημείο εκτελεί α.α.τ. Να αντιστοιχίσετε τα παρακάτω μεγέθη με τα αντίστοιχα διαγράμματα.α. Ενέργεια ταλάντωσης
β. Δυναμική ενέργεια ταλάντωσης
γ. Κινητική ενέργεια ταλάντωσης
7. Στο παρακάτω σχήμα φαίνεται η μεταβολή της φάσης μιας α.α.τ. σε συνάρτηση με το χρόνο. Ποιες από τις επόμενες προτάσεις είναι σωστές;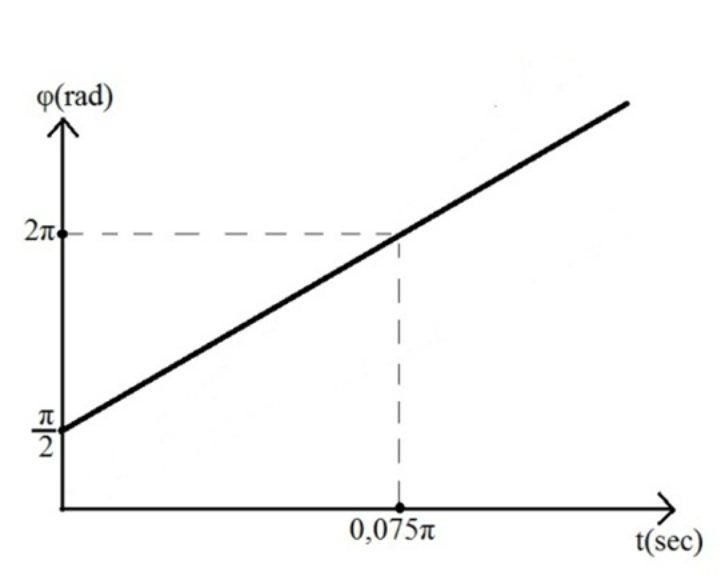
8. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές; Σε μια α.α.τ. περιόδου \[T\] και πλάτους \[A\]: 11. Σύστημα ελατήριο-σώμα του παρακάτω σχήματος τίθεται σε κίνηση.
12. Σε μια α.α.τ. ο ταλαντωτής περνά απ’ τα σημεία Γ και Δ της τροχιάς του με μη μηδενική ταχύτητα. Τα σημεία αυτά είναι συμμετρικά ως προς τη Θ.Ι. της ταλάντωσης.Α. Για την επιτάχυνση του ταλαντωτή στις θέσεις Γ και Δ ισχύει:
α. \[α_Γ=α_Δ\]. β. \[α_Γ=-α_Δ\]. γ. \[α_Γ=α_Δ=α_{max}\]. δ. \[|α_Γ|=2|α_Δ|\].
Β. Για τις κινητικές ενέργειες του ταλαντωτή στις θέσεις Γ και Δ ισχύει:
α. \[Κ_Γ=Κ_Δ\]. β. \[Κ_Γ=Κ_Δ=0\]. γ. \[Κ_Γ=Κ_Δ=Κ_{max}\]. δ. \[Κ_Γ \neq Κ_Δ\].
15. Η δυναμική ενέργεια της α.α.τ. με περίοδο Τ γίνεται ίση με την κινητική της: 18. Στο παρακάτω σχήμα φαίνονται τα διαγράμματα της απομάκρυνσης δύο ταλαντωτών \[(1)\], \[(2)\] σε σχέση με το χρόνο. Οι ταλαντωτές έχουν ίσες μάζες.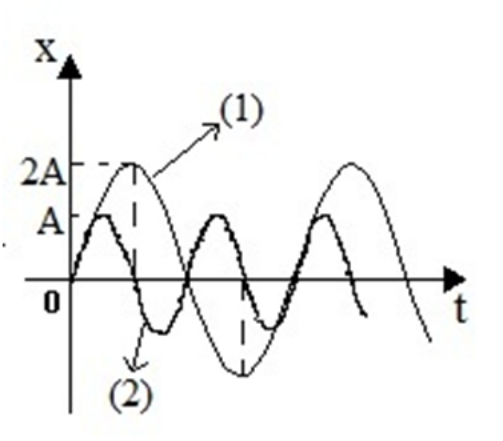
Α. Για τις μέγιστες επιταχύνσεις των δύο ταλαντωτών ισχύει:
α. \[α_{max,1}=2α_{max,2}\].
β. \[α_{max,1}=\frac{ α_{max,2} }{2}\].
γ. \[α_{max,1}=4α_{max,2}\].
δ. \[ α_{max,1}=\frac{α_{max,2}}{4}\].
B. Για τις μέγιστες δυναμικές ενέργειες των δύο ταλαντωτών ισχύει:
α. \[U_{Tmax,1}=U_{Tmax,2}\].
β. \[U_{Tmax,1}=\frac{U_{Tmax,2}}{2}\].
γ. \[U_{Tmax,1}=2U_{Tmax,2}\].
δ. \[U_{Tmax,1}=4U_{Tmax,2}\].
20. Σε κάθε φθίνουσα μηχανική ταλάντωση: 21. Τα σώματα \[Σ_1\] και \[Σ_2\] του παρακάτω σχήματος έχουν μάζες \[m_1=m\] και \[m_2=2m\] αντίστοιχα και ηρεμούν στερεωμένα στα άκρα ιδανικών ελατηρίων πάνω σε λείο οριζόντιο δάπεδο. Τα ελατήρια έχουν σταθερές επαναφοράς \[k_1=k\] και \[k_2=2k\]. Εκτρέπω τα σώματα κατά τη διεύθυνση των αξόνων των ελατηρίων κατά \[x_0\] και \[2x_0\] αντίστοιχα προς τα δεξιά και την \[t=0\] τα αφήνω ελεύθερα. Τα σώματα εκτελούν α.α.τ. Τη στιγμή \[t_1\] και \[t_2\] αντίστοιχα τα σώματα \[Σ_1\], \[Σ_2\] περνούν απ’ τη Θ.Ι. τους για πρώτη φορά μετά τη στιγμή \[t=0\].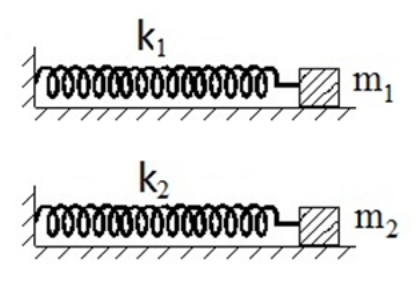
A. Για τους χρόνους , ισχύει:
α. \[t_1=2t_2\]. β. \[ t_1=4t_2\]. γ. \[t_1=t_2\]. δ. \[t_1=\frac{t_2}{2} \]. Β. Για τις ενέργειες των δύο ταλαντωτών ισχύει:
α. \[Ε_{Τ,1}=\frac{ Ε_{Τ,2} }{8} \].
β. \[Ε_{Τ,1}=2Ε_{Τ,2}\].
γ. \[Ε_{Τ,1}=\frac{Ε_{Τ,2} }{4} \].
δ. \[Ε_{Τ,1}=Ε_{Τ,2} \].
22. Επιλέξτε ποιες απ’ τις παρακάτω προτάσεις είναι σωστές. Σε μια α.α.τ. η δύναμη επαναφοράς: 23. Η περίοδος ενός περιοδικού φαινομένου είναι \[2\; s\]. Αυτό σημαίνει: 24. Το σώμα μάζας \[m\] του παρακάτω σχήματος ισορροπεί στο πάνω άκρο κατακόρυφου ελατηρίου σταθεράς \[k\]. Εκτρέπω το σώμα κατά \[y_0\] κατακόρυφα προς τα κάτω και απ’ τη θέση αυτή το αφήνω ελεύθερο να εκτελέσει α.α.τ. Η ενέργεια που δαπάνησα είναι \[Ε_1\] ενώ το σώμα επιστρέφει για πρώτη φορά στη Θ.Ι. του μετά απ’ τη στιγμή που το άφησα σε χρονικό διάστημα \[Δt_1\]. Αντικαθιστώ το ελατήριο με ένα δεύτερο σταθεράς \[k_2=4k_1\] και επαναλαμβάνω το ίδιο πείραμα εκτρέποντας το σώμα κατά το ίδιο \[y_0\]. Τώρα δαπάνησα ενέργεια \[E_2\] και ο ταλαντωτής επιστρέφει στη Θ.Ι. του για πρώτη φορά σε χρονικό διάστημα \[Δt_2\].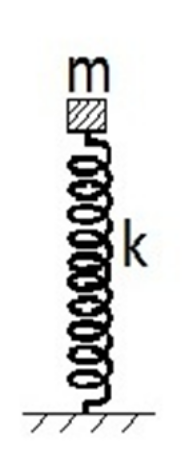
Α. Για τις δαπανώμενες ενέργειες ισχύει:
α. \[Ε_1=4Ε_2\]. β. \[Ε_1=16Ε_2\]. γ. \[Ε_1=2Ε_2\]. δ. \[Ε_1=\frac{Ε_2}{4} \].
Β. Για τα χρονικά διαστήματα ισχύει:
α. \[Δt_1=Δt_2\].
β. \[Δt_1=4Δt_2\].
γ. \[Δt_1=2Δt_2\].
δ. \[ Δt_1=\frac{ Δt_2 }{ \sqrt{2} }\].
25. Σώμα εκτελεί φθίνουσα μηχανική ταλάντωση, την \[t=0\] έχει πλάτος \[Α_0\] και η χρονική μεταβολή του πλάτους του δίνεται απ’ τη σχέση \[ A=A_0 e^{-Λt} \] όπου \[Λ\] μια θετική σταθερά. Να αντιστοιχήσετε τις συναρτήσεις του πλάτους \[A=f(t)\] και της ενέργειας \[E_T=f(t)\] με τα διαγράμματα της δεύτερης στήλης.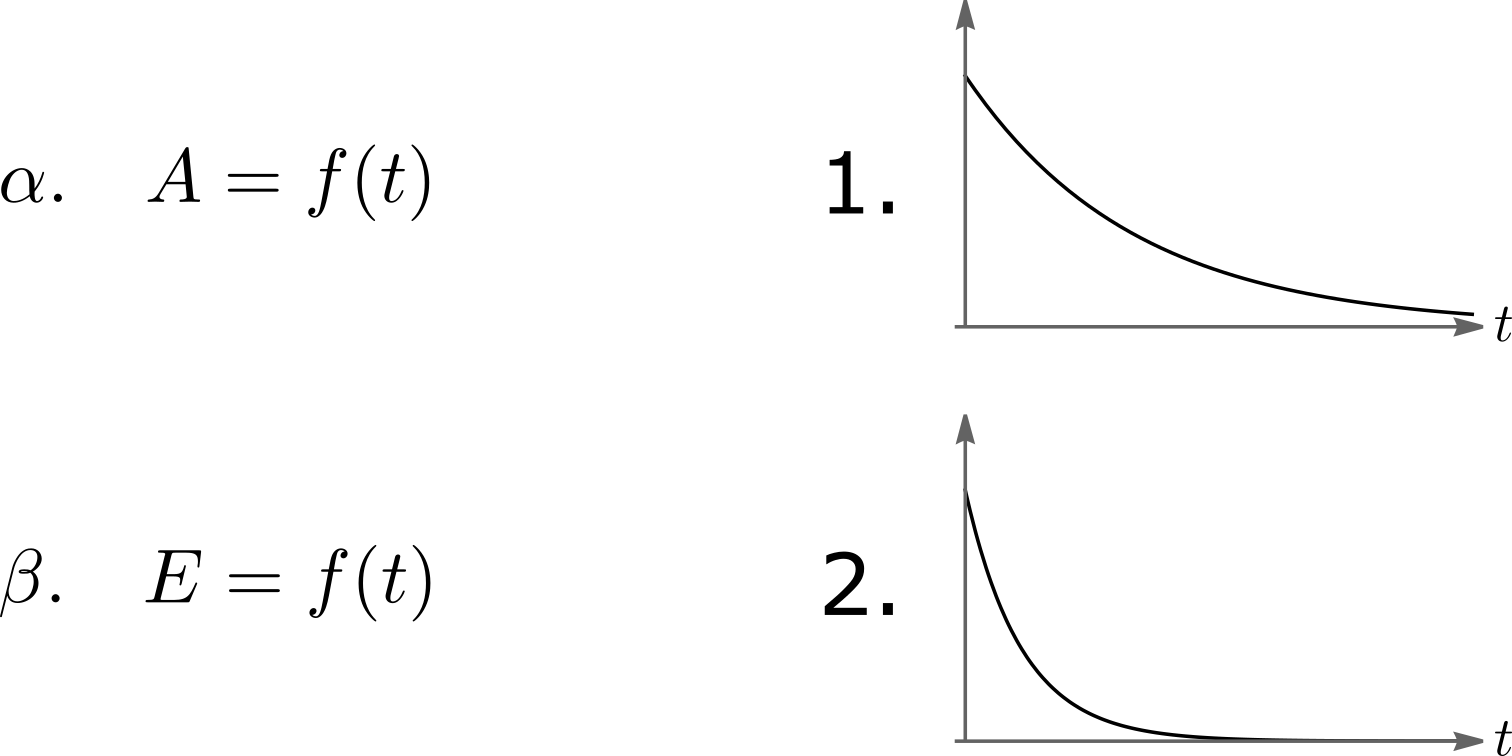
26. Στο παρακάτω σχήμα φαίνονται σε κοινό σύστημα αξόνων τα διαγράμματα της δυναμικής, κινητικής, ολικής ενέργειας μιας απλής αρμονικής ταλάντωσης πλάτους Α και περιόδου Τ.
Α. Η δυναμική ενέργεια της α.α.τ. περιγράφεται στο διάγραμμα:
α. \[1\]. β. \[2\]. γ. \[3\].
Β. Οι τιμές των \[x_1,x_2\] είναι:
α. \[\pm \frac{A}{2}\]. β. \[\pm \frac{A\sqrt{2} }{2}\]. γ. \[\pm \frac{A\sqrt{3}}{2}\]. δ. \[ x_1=-\frac{A}{2}\, ,\, x_2=+\frac{A\sqrt{2} }{2} \].
