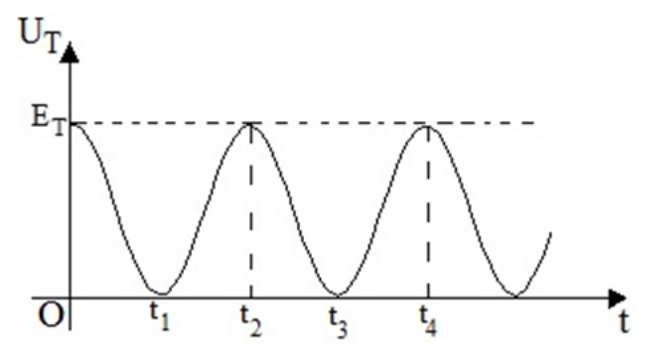
4. Στο παρακάτω διάγραμμα φαίνεται η μεταβολή της δύναμης επαναφοράς που δέχεται ένας ταλαντωτής που εκτελεί α.α.τ. Ποιες από τις παρακάτω προτάσεις είναι σωστές;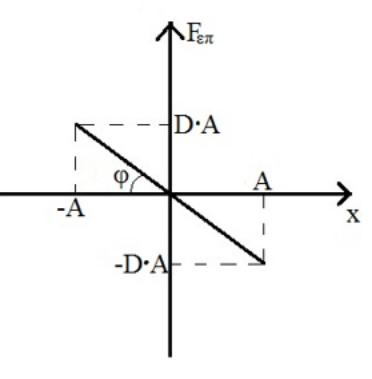
9. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές; Η επιτάχυνση σε μια α.α.τ. 11. Στο παρακάτω σχήμα φαίνονται οι γραφικές παραστάσεις των επιταχύνσεων σε συνάρτηση με την απομάκρυνσή τους για δύο απλούς αρμονικούς ταλαντωτές με μάζες \[m_1\] και \[2m_1\] αντίστοιχα.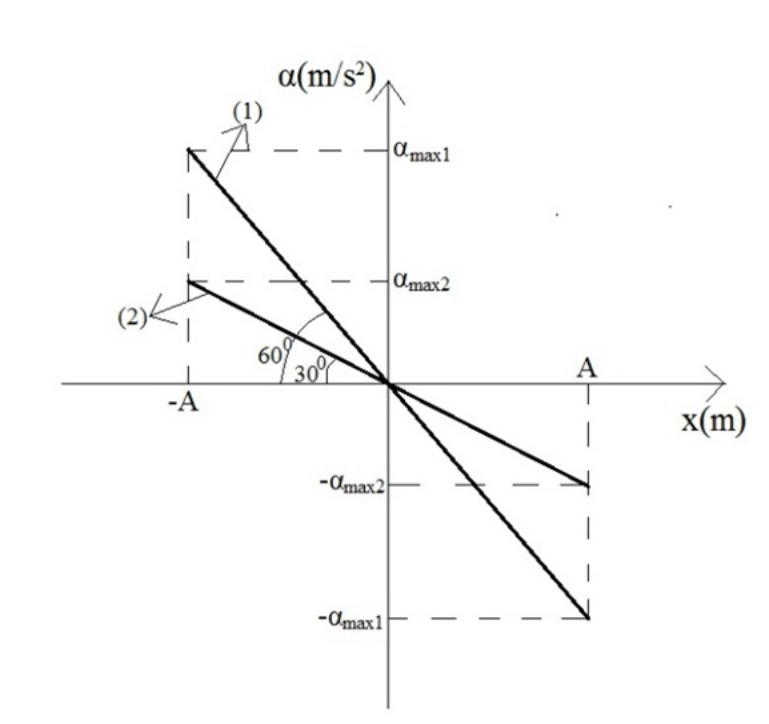
Α. Ο λόγος των γωνιακών συχνοτήτων για τους δύο ταλαντωτές είναι:
α. \[ \frac{ω_1}{ω_2} =\sqrt{3} \].
β. \[ \frac{ω_1}{ω_2} =\frac{\sqrt{3} }{3}\].
γ. \[ \frac{ω_1}{ω_2} =3\].
δ. \[ \frac{ω_1}{ω_2} =\frac{1}{3} \].
Β. Ο λόγος των ενεργειών των δύο α.α.τ. είναι:
α. \[\frac{ Ε_{Τ,1} }{ Ε_{Τ,2} } =\frac{1}{2}\].
β. \[ \frac{ Ε_{Τ,1} }{ Ε_{Τ,2} } =\frac{ 3}{ 2}\].
γ. \[ \frac{ Ε_{Τ,1} } {Ε_{Τ,2} } =\frac{2}{3} \].
δ. \[ \frac{ Ε_{Τ,1} }{Ε_{Τ,2} } =\frac{9}{2} \].
13. Σώμα εκτελεί α.α.τ. Στο παρακάτω σχήμα φαίνεται το διάγραμμα της μεταβολής της επιτάχυνσης του ταλαντωτή σε συνάρτηση με το χρόνο. Ποιες από τις επόμενες προτάσεις είναι σωστές;
16. Υλικό σημείο εκτελεί α.α.τ. μεταξύ των ακραίων θέσεων Κ, Λ γύρω απ’ τη θέση ισορροπίας Ο. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Το έργο της δύναμης επαναφοράς:
17. Τα σώματα \[Σ_1\], \[Σ_2\] ισορροπούν στα πάνω άκρα κατακόρυφων ιδανικών ελατηρίων σταθεράς \[k_1\, ,\, k_2\] που τα άλλα άκρα τους είναι στερεωμένα σε οριζόντιο δάπεδο. Τα σώματα έχουν ίσες μάζες. Εκτοξεύω τα δύο σώματα απ’ τις Θ.Ι. τους με κατακόρυφες ταχύτητες μέτρων \[υ_1\] και \[υ_2=\frac{υ_1}{2}\] αντίστοιχα και αυτά αρχίζουν να εκτελούν α.α.τ. Παρατηρώ ότι τη στιγμή που το \[Σ_1\] επιστρέφει στη Θ.Ι. του για 1η φορά μετά την εκτόξευση του, το \[Σ_2\] ακινητοποιείται για πρώτη φορά.Α. Για τις σταθερές των ελατηρίων \[k_1\, ,\, k_2\] ισχύει:
α. \[k_1=k_2 \sqrt{2}\].
β. \[k_1=4k_2\].
γ. \[k_1=\frac{k_2}{4}\].
δ. \[k_1=\frac{k_2}{ \sqrt{2} }\].
Β. Για τις μέγιστες επιταχύνσεις των σωμάτων \[α_{max,1}\, ,\, α_{max,2}\] ισχύει:
α. \[α_{max,1}=α_{max,2}\].
β. \[α_{max,1}=2α_{max,2}\].
γ. \[α_{max,1}=4α_{max,2}\].
δ. \[α_{max,1}=\sqrt{2} α_{max,2}\].
19. Σε μια φθίνουσα μηχανική ταλάντωση, η δύναμη που αντιστέκεται στην κίνηση είναι της μορφής \[F_{αν}=-bυ\] όπου \[υ\] η αλγεβρική τιμή της ταχύτητας και \[b\] μια θετική σταθερά. Στη διάρκεια μιας περιόδου το μέτρο της αντιτιθέμενης δύναμης \[F_{αν}\]: 21. Ένα κρυστάλλινο ποτήρι μπορεί να σπάσει λόγω ενός ηχητικού κύματος όταν: 25. Σώμα εκτελεί α.α.τ. Στο παρακάτω σχήμα φαίνεται το διάγραμμα της μεταβολής της απομάκρυνσης του ταλαντωτή απ’ τη Θ.Ι. του σε συνάρτηση με το χρόνο. Ποιες από τις επόμενες προτάσεις είναι σωστές;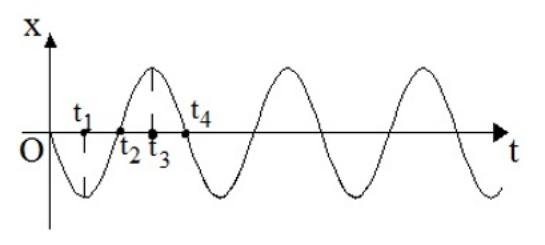
27. Το σώμα \[Σ_1\] μάζας \[m_1\] του διπλανού σχήματος εκτελεί α.α.τ. Στη θέση \[x_0\] πάνω απ’ τη Θ.Ι. του, τη στιγμή που κατέρχεται, συγκρούεται μετωπικά και πλαστικά με σώμα \[Σ_2\] που ανέρχεται με ταχύτητα \[υ_2\]. Αμέσως μετά την κρούση το συσσωμάτωμα ακινητοποιείται στιγμιαία και κατόπιν εκτελεί α.α.τ. Για την α.α.τ. του συσσωματώματος ισχύει: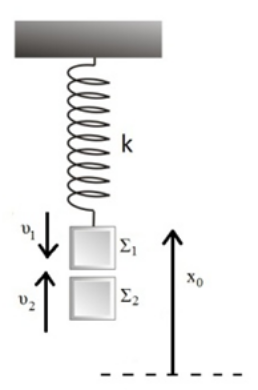
28. Στο παρακάτω διάγραμμα φαίνεται η μεταβολή της δυναμικής ενέργειας του ταλαντωτή σε συνάρτηση με το χρόνο. Ποιες από τις επόμενες προτάσεις είναι σωστές;