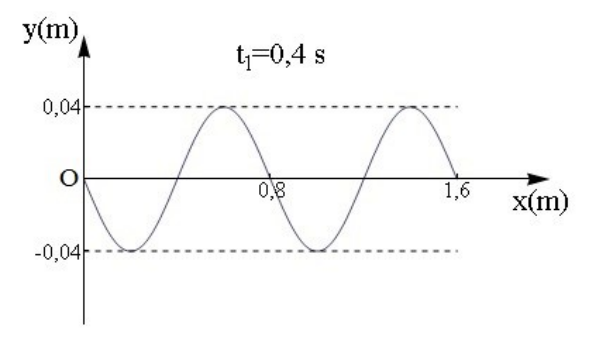
6. Ένα αρμονικό κύμα σε γραμμικό ελαστικό μέσο διαδίδεται: 8. Εγκάρσιο αρμονικό κύμα διαδίδεται στη διεύθυνση του άξονα \[x' Ox\] κατά την αρνητική φορά και χωρίς αρχική φάση. Στο παρακάτω διάγραμμα φαίνεται η χρονική συνάρτηση της απομάκρυνσης σημείου Ζ του μέσου διάδοσης. Το σημείο Ζ είναι το δεύτερο σημείο κατά τη φορά διάδοσης του κύματος μετά την αρχή Ο που έχει κάθε στιγμή στη διάρκεια της ταλάντωσής του ίδια απομάκρυνση και ταχύτητα με την Ο. Η ταχύτητα διάδοσης του κύματος είναι \[υ_δ=4\, \frac{m}{s} \]. Η εξίσωση του κύματος είναι: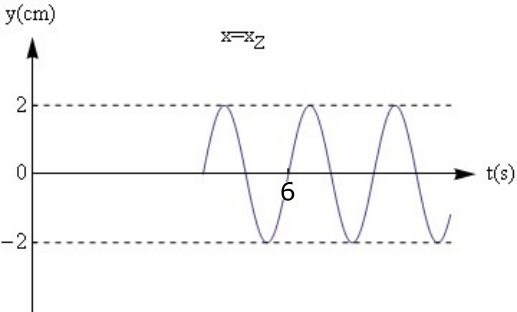
10. Δύο σύγχρονες πηγές κυμάτων δημιουργούν πάνω στην επιφάνεια υγρού εγκάρσια αρμονικά κύματα ίδιου πλάτους Α και χωρίς αρχική φάση. Τα σημεία της επιφάνειας στα οποία παρουσιάζεται ενίσχυση και δεν ισαπέχουν απ’ τις δύο πηγές, τη στιγμή που αρχίζει η συμβολή σ’ αυτά: 15. Κατά μήκος δύο διαφορετικών χορδών (1) και (2) δημιουργούνται από δύο πανομοιότυπες πηγές εγκάρσια αρμονικά κύματα ίδιου πλάτους, με μήκη κύματος \[λ_1\, ,\, λ_2\] αντίστοιχα για τα οποία ισχύει \[λ_1=2λ_2\]. Αν \[α_{max,1}\] και \[α_{max,2}\] είναι οι μέγιστες επιταχύνσεις ταλάντωσης των σημείων των χορδών τότε ισχύει: 16. Κατά μήκος δύο πανομοιότυπων χορδών (1) και (2) δημιουργούνται εγκάρσια αρμονικά κύματα ίδιου πλάτους με μήκη κύματος \[λ_1\, , \, λ_2\] αντίστοιχα για τα οποία ισχύει \[λ_1=2λ_2\]. Αν \[υ_{max,1}\] και \[υ_{max,2}\] είναι οι μέγιστες ταχύτητες ταλάντωσης των σημείων των χορδών τότε ισχύει: 18. Κατά μήκος ελαστικής χορδής διαδίδεται αρμονικό κύμα μήκους κύματος \[λ\]. Δύο σημεία απέχουν μεταξύ τους \[Δx=\frac{5λ}{2}\]. Μετά την έναρξη της ταλάντωσής τους: 21. Δύο σύγχρονες πηγές κυμάτων αρχίζουν να ταλαντώνονται με θετική ταχύτητα και δημιουργούν στην επιφάνεια υγρού εγκάρσια αρμονικά κύματα ίδιου πλάτους \[Α\], περιόδου \[Τ\] και μήκους κύματος \[λ\]. Σε σημείο Κ της επιφάνειας η συμβολή αρχίζει τη χρονική στιγμή \[t_Σ\]. Στο Κ εμφανίζεται ενίσχυση. Ποιες από τις παρακάτω προτάσεις είναι σωστές; 22. Δύο σύγχρονες πηγές κυμάτων \[Π_1\, , \, Π_2 \] δημιουργούν στην επιφάνεια υγρού εγκάρσια αρμονικά κύματα ίδιου πλάτους \[Α\] και μήκους κύματος \[λ\]. Αν σημείο Σ της επιφάνειας απέχει απ’ τις πηγές \[Π_1\, , \, Π_2\] αποστάσεις \[r_1\, ,\, r_2\] αντίστοιχα, τότε το σημείο Σ ταλαντώνεται μετά τη συμβολή με μέγιστο πλάτος μόνο αν: 29. Εγκάρσιο αρμονικό κύμα διαδίδεται σε ομογενές ελαστικό μέσο που ταυτίζεται με τη διεύθυνση του \[x' x\] κατά τη θετική φορά. Η εξίσωση της ταλάντωσης της αρχής του άξονα Ο έχει τη μορφή \[y=A\, ημωt\]. Στο παρακάτω σχήμα φαίνεται το στιγμιότυπο του κύματος τη στιγμή \[t_1=0,4\, s\]. Η εξίσωση που περιγράφει το κύμα είναι: